训练
水果数据
| 直径 | 颜色 | 水果 |
| 4 | Red | Apple |
| 4 | Green | Apple |
| 1 | Red | Cherry |
| 1 | Green | Grape |
| 5 | []Red | Apple |
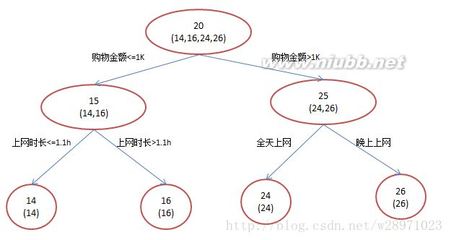
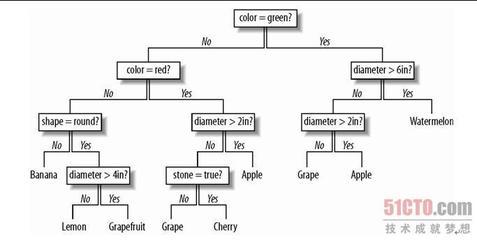
为了创建树的根节点,有两个可能的变量可用于对数据进行拆分,它们分别是直径和颜色。第一步就是要对每个变量都进行尝试,从中找出拆分数据效果最好的一个。按照颜色拆分数据集得到的结果如下图
| Red | Green |
| Apple | Apple |
| Cherry | Grape |
| Apple |
上述数据依然显得非常混乱。但是,假如我们按直径(小于4英寸、大于或等于4英寸)进行拆分,则拆分得到的结果会变得非常清晰(我们将左侧的数据成为Subset1,右侧的数据成为Subset2).此时的拆分情况如下图所示
| 直径<4英寸 | 直径≥4英寸 |
| Cherry | Apple |
| Grape | Apple |
这显然是一种更好的拆分结果,因为Subset2包含来自初始集合的所有“Apple”条目。尽管在本例中,哪个变量的拆分效果更好是明确的;但是当面对规模更大一些的数据集时,就不会总是有如此清晰的拆分结果了。为了衡量一个拆分的优劣。引入了一个熵的概念(代表一个集合中无序的程序):集合中的熵偏小,就意味着该集合中的大部分元素都是同质的;而熵等于0,则代表集合中的所有元素都是同一类型的。在上图中Subset2(直径≥4)的熵即为0.每个集合中的熵都是用来计算信息增益的,信息增益定义如下:因此对于每一种可能的拆分,我们都会计算出相应的信息增益,并以此来确定拆分用的变量。一旦用以拆分的变量被选定,第一个节点就创建出来了。 diameter ≥4min ? yes noCherry(1,Red) AppleGrape(1,Green)
因此,我们将判断条件显示在了节点的位置,如果数据不满足判断条件,就会沿着no分支向下走,如果满足,则会沿着yes分支向下走。因为yes分支现在仅有一种可能的结果,因此它就成了叶节点。no分支依然显得有些混乱,因此可以采用与选择跟节点时完全相同的办法对其做进一步的拆分。在本例中,颜色现在成了拆分数据的最佳变量。这一过程会一直重下去,直到在某个分支上拆分数据时不会再有信息增益为止。
决策树分类器使用说明
决策树算法的实现是基于一个列表的列表进行训练的,每个内部列表都包含了一组值,其中的最后一个值代表分类。我们可以按如下所示的方法来创建前面那个简单的水果数据集。fruit =[[4,'red','apple'],[4,'green','apple'],[1,'red','cherry'],[1,'green','grape'],[5,'red','apple']]
现在我们可以对这颗决策树进行训练,并利用它对新的样本进行分类:importtreepredicttree =treepredict.buildtree(fruit)treepredict.classify([2,'red'],tree){'cherry':1}treepredict.classify([5,'red'],tree){'apple':3}treepredict.classify([1,'green'],tree){'grape':1}treepredict.classify([120,'red'],tree){'apple':3}
很显然,直径10英寸并且颜色为紫色的水果不应该是苹果,但决策树受制于其所见过的样本,最后我们可以将树打印或绘制出来,以理解其决策的推导过程:treepredict.printtree(tree)0:4?T->{'apple':3}F->1:green? T-> {'grape':1} F-> {'cherry':1}
优点和缺点
决策树最为显著的优点在于,利用它来解释一个受训模型是非常容易的,而且算法将最为重要的判断因素都很好地安排在了靠近树根部位置。这意味着,决策树不仅对分类很有价值,而且对决策过程的解释也很有帮助。像贝叶斯分类器一样,可以通过观察内部结构来理解它的工作方式,同时这也有助于在分类过程之外进一步作出其他的决策。
因为决策树要寻找能够使信息增益达到最大化的分界线,因此它也可以接受数值型数据作为输入。能够同时处理分类数据和数值数据,对于许多问题的处理都是很有帮助的--这些问题往往是传统的统计方法(比如回归)所难以应对的。另一方面,决策树并不擅长于对数值结果进行预测。一颗回归树可以将数据拆分成一系列具有最小方差的均值,但是如果数据非常复杂,则树就会变得非常庞大,以至于我们无法借此来作出准确的决策。
与贝叶斯决策树相比,决策树的主要优点是它能够很容易地处理变量之间的相互影响。一个用决策树构建的垃圾邮件过滤器可以很容易的判断出:"onlie" 和 "pharmacy" 在分开时并不代表垃圾信息,担当它们组合在一起时则为垃圾信息。
 爱华网
爱华网