AAAAAAAAAAAAAAAAAAAAAAAA
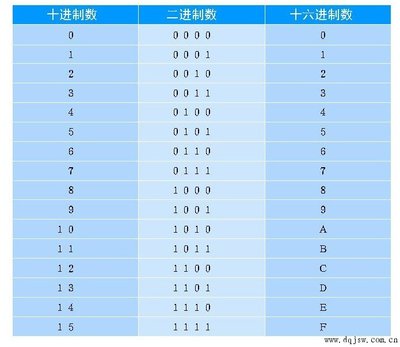
1 NNNNNU NNNNNAAA NNNNN.NNNNNNNN +.NNNNNNNN +NNNNN-N +NNNNN-N NNNNNN
2 NNNNN NNN.NNNN NNN.NNNN NNNNNNN NNN.NNNN NNN.NNNNNN.NNNNNNNNNNNNNN第0行是一个24字符的名字,后两行分别代表的含义为:
第 1行 | |
列 | 描述 |
01 | 行号 |
03-07 | 卫星编号 |
08 | 保密分级(U=非保密的) |
10-11 | 国际标志符(发射年份后两位数字) |
12-14 | 国际标志符(那一年的发射编号) |
15-17 | 国际标志符(那次发射的件编号) |
19-20 | TLE历时(年份后两位数) |
21-32 | TLE历时(用一个十进制小数表示的一年中的第几日和日中的小数部分) |
34-43 | 平均运动的一阶时间导数 |
45---52 | 平均运动的二阶时间导数(小数点的位置已确定) |
54-61 | BSTAR阻力系数(小数点位置已确定) |
63 | 星历表类型 |
65-68 | 星历编号 |
69 | 校验和(以10为模) |
第2行 | |
列 | 描述 |
01 | 行号 |
03-07 | 卫星编号 |
09-16 | 轨道的交角[度数] |
18-25 | 升交点赤经 [度数] |
27-33 | 离心率 (小数) |
35-42 | 近地点角距[度数] |
44-51 | 平近点角[度数] |
53-63 | 平均运动[每日绕行圈数] |
64-68 | 在轨圈数 |
69 | 校验和(以10为模) (对于非数字部分:字母, 空格,句点, 正号 = 0; 负号 = 1) |
1 31800U 07031A 07186.84787415-.00000110 00000-0 00000+0015
2 31800 24.2268 102.4131 7891523 179.2824183.75791.5636312016
很多的卫星数据都可以在http://celestrak.com/查询星历的具体的详细的说明,见:http://celestrak.com/columns/v04n03/将两行星历拷贝到一个文件中。转换成轨道六根数的MATLAB程序如下:
%function [oe,epoch,yr,M,E,satname] = TLE2oe(fname);
%fname is a filename string for a file containing
%a two-line element set (TLE)
%oe is a 1/6 matrix containing the orbital elements
%[a e i Om om nu]
%yr is the two-digit year
%M is the mean anomaly at epoch
%E is the eccentric anomaly at epoch
%satname is the satellite name
%
% Calls Newton iteration function file EofMe.m
function[oe,epoch,yr,M,E,satname] = TLE2oe(file1.txt);
% Open the fileup and scan in the elements
fid =fopen(fname, 'r');
A = fscanf(fid,'%13c%*s',1);
B =fscanf(fid,'%d%6d%*c%5d%*3c%2d%f%f%5d%*c%*d%5d%*c%*d%d%5d',[1,10]);
C = fscanf(fid,'%d%6d%f%f%f%f%f%f',[1,8]);
fclose(fid);
satname=A;
% The value ofmu is for the earth
mu = 3.986004415e5;
% Calculate2-digit year (Oh no!, look out for Y2K bug!)
yr =B(1,4);
% Calculateepoch in julian days
epoch = B(1,5);
%ndot = B(1,6);
% n2dot = B(1,7);
% Assignvariables to the orbital elements
i =C(1,3)*pi/180;% inclination
Om =C(1,4)*pi/180;% Right Ascension of the Ascending Node
e =C(1,5)/1e7;% Eccentricity
om =C(1,6)*pi/180;% Argument of periapsis
M =C(1,7)*pi/180;% Mean anomaly
n = C(1,8)*2*pi/(24*3600); % Meanmotion
% Calculate thesemi-major axis
a = (mu/n^2)^(1/3);
% Calculate theeccentric anomaly using mean anomaly
E = EofMe(M,e,1e-10);
% Calculatetrue anomaly from eccentric anomaly
cosnu = (e-cos(E)) / (e*cos(E)-1);
sinnu = ((a*sqrt(1-e*e)) / (a*(1-e*cos(E))))*sin(E);
nu = atan2(sinnu,cosnu);
if (nu<0), nu=nu+2*pi; end
% Return theorbital elements in a 1x6 matrix
oe = [a e i Om om nu];
另外一个需要的程序为:
% this function solves Kepler'sequation,
% computing E as a function of M and e
%
function E = EofMe(M,e,tol)
if ( nargin<3 ), tol=1e-11;end
En = M;
En1 = En -(En-e*sin(En)-M)/(1-e*cos(En));
while ( abs(En1-En) > tol )
En = En1;
En1 = En -(En-e*sin(En)-M)/(1-e*cos(En));
end;
E = En1;
 爱华网
爱华网