主成分分析---是因子分析的一种
作用:设法将原来众多具有一定相关性的指标,重新组合成一组新的互相无关————的综合指标来代替原来的指标。
步骤:分析--降维-因子分析-选择进行主成分分析的变量
单击“描述”按钮可选定进行检验,“抽取”按钮中可设置抽取标准,通常是基于特征值大于1
单击“旋转”按钮选定,旋转方法,改变方法可轻微修改累积方差%
主成分分析方法需要注意:
1.经过KMO检验和Bartlett检验
KMO统计量是取值在0和1之间。当所有变量间的简单相关系数平方和远远大于偏相关系数平方和时,KMO值接近1.KMO值越接近于1,意味着变量间的相关性越强,原有变量越适合作因子分析;当所有变量间的简单相关系数平方和接近0时,KMO值接近0.KMO值越接近于0,意味着变量间的相关性越弱,原有变量越不适合作因子分析。 常用的kmo度量标准: 0.9以上表示非常适合;0.8表示适合;0.7表示一般;0.6表示不太适合;0.5以下表示极不适合。一般在0.8左右可以接受
Bartlett检验显著性 SIG <0.05 才可以接受
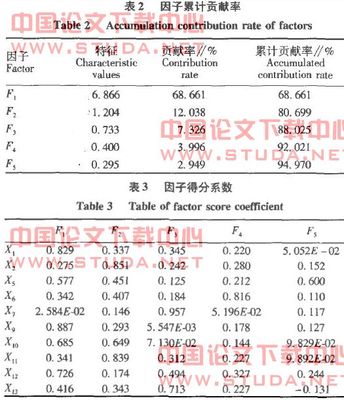
2.累积方差贡献率应在80%以上
在已有变量的基础上,经过多次尝试,去除“公因子方差”表中提取值较低的指标,能有效提高累积方差贡献率。
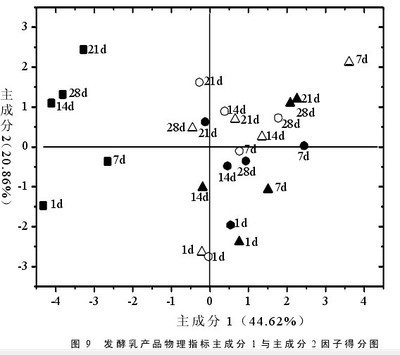
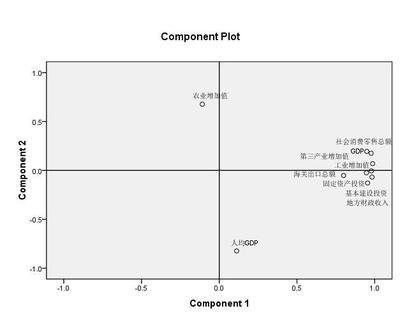
最终的成果主要是旋转矩阵,如下确定为2个主成分。各指标两个主成分下的数值,表示相互关系的紧密程度,负数表示为反向关系。同一指标在成分1和成分2下,绝对值较大的,可归为此成分。
将主成分分析的值代入,可计算总的综合评价值,从而可进一步进行聚类分析等等。
 爱华网
爱华网