阳城县第三中学王晓军
课型:新授
教学目标:
一、知识与技能目标
(1)能根据一次函数的图象和函数关系式,探索并理解一次函数的增减性;
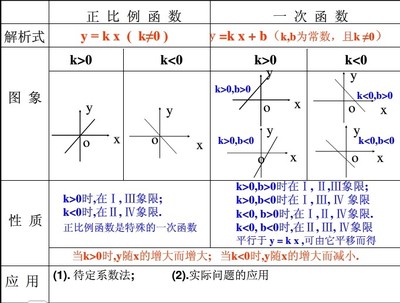
(2)进一步理解正比例函数图象和一次函数图象的位置关系;
(3)探索一次函数的图象在平面直角坐标系中的位置特征。
二、过程与方法目标
通过组织学生参与由一次函数的图象来揭示函数性质的探索活动,培养学生观察、比较、抽象和概括的能力,培养学生用数形结合的思想方法探索数学问题的能力。
三、情感、态度与价值观目标
通过师生共同探讨,体现数学学习充满着探索性和创造性,感受共同合作取得成功的快乐。
教学重点:一次函数图象的性质。
教学难点:通过图形探求性质以及分析图形的位置特征。
课前准备:
本节课为了帮助同学们能正确理解函数的增减性,更清楚、快捷地通过图象探究函数的某些特征。教师在课前准备好多媒体课件,并选择在多媒体教室完成本节课的教学任务。
教材分析:
华师版八年级《数学》下册一次函数图象的性质一课,在教材的设计上,充分挖掘学生生活实际中的登山实例,引导学生通过感受图形的上升与下降,激发学生探索问题的欲望,从而主动去寻找一次函数的图象在上升与下降的状况中,两变量之间的变化规律,并在此基础上,归纳出一次函数的增减性。
教材在课程设计上,鼓励学生自主探究和交流合作,改变老教材较注重传授,而学生只是单纯的通过记忆获取知识,并依赖模仿去学习解决问题的方法。
一次函数的图象和性质,对学生来说是一个全新的学习内容,也是初中分阶段数学学习的一个重要基础内容。对初学者来说,如果在研究新知识的过程中,形成自己对数学知识的正确理解,和掌握有效的学习函数知识的模式,并在学习的过程中使数形结合的思维能力得到发展,学生就能很快接受所学内容,并能运用所学知识,灵活解决函数问题,从而避免同学们在数学学习中过早出现两级分化的现象。教材在这节数学内容的课程设计上的成功之处正在于此。
【教学过程设计】
一、创设情景,引导探究
(1)复习一次函数图象的画法
师:上节课我们了解了一次函数图象,并学习了图象的画法-----两点法。
同学们能画出函数y=-2x+4和y= -2x的图象吗?说说看,如何画?
生甲:能。因为一次函数的图象是一直线,所以,我可以过(2,0)和(0,4)两点画直线y=-2x+4。过(0,0)、(1,-2)两点画直线y=-2x。
师:很好。还有不同的取点方法吗?
生乙:有,可经过(1,2)和(0,4),画直线y=-2x+4;经过(1,-2)和(2,-4)画直线y= -2x。
师:大家说说看,哪一种取点法更好呢?
众:甲的方法好。
师:对。我们可以针对函数中不同的k和b的值,灵活取值。但是,通常这两个点我们一般描在坐标轴上,这样比较准确一些。
教师要求学生画出这两函数的图象。
【设计说明】通过对两函数图象画法的讨论,引导学生得出简捷画法,并为后面新知识的研究作一些伏笔。
(2)一次函数图象平行的特征
师:在前面问题的探究过程中,我们已知道,函数中k、b的正负,决定着图象的位置,那么如果几个函数的k相同,图象会怎样呢?(教师作承上启下的引导,此时学生必定很想去探究这一问题。)
师:我们一起来研究一次函数y1=2x,y2=2x+3,y3=2x-3的图象。
①指导大家填写下表,并观察表中数值的变化。
x | 1 | 2 | 3 | 4 | 5 | … |
y1=2x | ||||||
y2=2x+3 | ||||||
y3=2x-3 |
师:对应于同一自变量的值,三个函数的值有什么关系?
生:y2比y1大3,而y3比y1小3。
②师:请同学们在同一坐标系中画出3个函数的图象,作进一步的观察,并互相交流一下。
师:你们画出的图象有什么位置特征吗?
众:三条直线平行。
师:因此,我们可以如何得到一次函数y2=2x+3和y3=2x-3的图象呢?
生:是把y1=2x的图象向上或向下平移三个单位得到的。
师:很好。能否把这二结论推广到一般情形呢?
教师引导学生说出各自的结论,然后用多媒体展现这一结论。
二、师生互动,合作交流
(1)探究一次函数的增减性
(教师用多媒体呈现给大家一幅画面。图画上有两个一次函数的图象,而背景是一座山,两一次函数的图象正好对应着背景图中的上山和下山的路线,教师在课件中设计一个骑着自行车的人从左边上山顶,并继续下山到右边山脚,并把这一活动来回放两遍给学生看,继而引导学生思考)
师:在这一过程中,同学们看到了什么?
生:看到骑自行车的人从左边上山和下山的过程。
师:仔细想想看,在这一过程中,有哪些量发生了变化?
学生此时会说出各种不同的答案,比如路程变化了,比如高度变化了,教师引导学生得出,上山时越走越高,下山时越走越低,再作进一步引导。
师:能把你的观察结果同对应的两个一次函数图象联系起来吗?再联系到我们前面画的几个一次函数的图象,你能得到什么结论?
生:在y=2x、y=2x+3、y=2x-3的图象中,y随x增大而增大,在y=-2x、y=-2x+4的图象中,y随x增大而减小。
师:很好。我们能否把这一结论推广到一般情况。
(教师此时可用多媒体展现出前一节课所画过的各种一次函数图象,并逐步把图象按k>0,k<0归类。)
引导学生观察思考,并寻求结论。
生:一次函数的图象可按k>0和k<0分类。
k>0时,图象从左向右是上升的,此时y的值随x的增大而增大;
k<0时,图象从左向右是下降的,此时y的值随x的增大而减小。
师:非常正确。教师用多媒体展现函现性质,并指出这就是一次函数的重要性质。
【设计说明】通过对生活中上山越走越高,下山越走越低这一情景再现,引导学生观察、对比,并进行联想,得出一次函数中两变量的变化规律,完成了对新知的探究过程。
(2)一次函数的图象与坐标轴交点的位置特征。
师:(教师作如下问题引导,并重新展现y=-2x+4和y= -2x图象)
我们画图时,所取的点有什么特点?
生:都在坐标轴上,都是图象与坐标轴的交点。
师:很好。那么,你们能从中得出来一次函数图象与坐标轴的交点坐标的方法吗?
生:可以。当x=0时,求出y的值,得出与y轴的交点。当y=0时,求出x的值,得出与x轴的交点。
师:非常正确。
(以上面的图象为例,继续提问,引导学生思考,互相交流)
师:图象被交点A分成了几部分?它们的变量有哪些不同的取值?
教师引导学生画出三部分图形,并分别找出它们每部分为x>0,x=0,x<0。再找出每部分对应的因变量y的值。
师:那么B点又如何呢?继续交流一下。
生:图象被B点也分成三部分,在x轴上方的部分y>0,在x轴上的B点y=0,在x轴下方的部分y<0。
师:归纳得很完整。你能否再结合自变量x的取值情况进行讨论呢?
生:当x﹥2时,y﹤0;x=2时,y=0;x﹤2时,y﹥0。
师:正确。大家可用同样的方法归纳A点的情况。
【设计说明】通过动手画图,并且进行观察比较,合作交流,使学生更清楚地认识一次函数图象的一些特征以及图形和变量之间的关系。
三、练习巩固
(1)教师用多媒体展现下列一组填空题:
1.当m时,一次函数y=(5-m)x+2中,y随x的增大而减小。
2.根据下列一次函数y=kx+b(k≠0)的图象,写出每个图的k、b的取值范围。
k__ 0,b___0k___0,b____0k___0,b____0 k___0,b____0
3.直线y=kx-3与y=5x平行,则k=时,y随x增大而。
4.函数y=mx-m的图象过(2,1)点,则m=,函数的图象与x轴的交点坐标为(, ),与y轴的交点坐标为(, )。
5.一次函数y=kx+b中,当k 0,b0时,图象不过第一象限。
(2)课本第39页,练习1,2。
【设计说明】教师通过这组题目的训练,可帮助学生对本节课所探究的问题作一回顾,同时也检验学生观察图形,运用所学知识的能力。
四、课堂小结
师:通过本节课的学习,我们理解了哪些一次函数的有关内容呢?
(1):一次函数图象的位置特征
(2):一次函数的增减性
五、布置作业
课本P41,习题18.3 4,5,6
六、课后反思
1.教师在本节课的教学中,要力求引导学生从事观察,善于分析、交流、归纳等探索活动,从而使学生形成对一次函数图象及其性质的认识和理解,感受到图象的变化规律与表达式中的常数k,b的关系,使学生对知识的掌握更具主动性。
2.在学生探索性质的过程中,教师要作恰当的引导,这样才能帮助同学们从对不同图象的比较、分析中,得出一些具有实质性内容的结论,并能在探索中提高识图、用图的能力,培养学生主动参与数学学习活动,乐于自主解决问题,并发表看法的习惯。同时,通过在图象中探索一次函数y=kx+b(k≠0)性质和位置特征,培养学生数形结合思想,发展学生形象思维能力。
 爱华网
爱华网



