平方根的定义及性质 平方根性质

分享人:谪仙大人来源:互联网2

平方根

求助编辑百科名片

平方根

平方根，又叫二次方根，对于非负实数来说，是指某个自乘结果等于的实数，表示为〔√￣〕，其中属于非负实数的平方根称算术平方根。一个正数有两个平方根；0只有一个平方根，就是0本身；负数没有平方根。例：9的平方根是±3 注：有时我们说的平方根指算术平方根。

平方根的定义及性质 平方根性质

目录

概括
公式定义
竖式运算
讲解知识教案
  1. 教学重点与难点分析
  2. 算术平方根,平方根的定义
学生用计算器求平方根教案
  1. 教学重点难点分析
  2. 教法建议
计算机科学
  1. 用Ruby求平方根
  2. C语言版求平方根
  3. 平方根表
概括
公式定义
竖式运算
讲解知识教案
  1. 教学重点与难点分析
  2. 算术平方根,平方根的定义
学生用计算器求平方根教案
  1. 教学重点难点分析
  2. 教法建议
计算机科学
  1. 用Ruby求平方根
  2. C语言版求平方根
  3. 平方根表
展开

编辑本段概括

　　一个正数如果有平方根，那么必定有两个，它们互为相反数。显然，如果我们知道了这两个平方根的一个，那么就可以及时的根据相反数的概念得到它的另一个平方根。　　如果一个数的平方等于a，那么这个数叫做a的平方根。0的平方根是0，负数的平方根为i（-1的平方根为i，-9的平方根为3i）。

编辑本段公式定义

　　若一个数x的平方等于a，即x^2=a,

编辑本段竖式运算

　　像加减乘除一样，求平方根也有自己的竖式运算。以求3的算术平方根为例，过程如右下图：解得3的算术平方根约为1.732

求算术平方根的竖式运算

　　1、因为每次补数需要补两位，所以被开方数不只一个数位时，要保证补数不能夹着小数点。例如三位数，必须单独用百位进行运算，补数时补上十位和个位的数。　　2、每一个过渡数都是由上一个过渡数变化而后，上一个过渡数的个位数乘以2，如果需要进位，则往前面进1，然后个位升十位，以此类推，而个位上补上新的运算数字。简单地讲，过渡数27，是第一次商的1乘以20，把个位上的0用第二次商的7来换，过渡数343是前两次商的17乘以20=340，其中个位0用第三次商的3来换，第三个过渡数3462是前三次商173乘以20=3460，把个位0用第四次的商2来换，依次类推。　　3、误差值的作用。如果要求精确到更高的小数数位，可以按规则，对误差值继续进行运算。

编辑本段讲解知识教案

教学重点与难点分析

　　本节重点是平方根和算术平方根的概念．平方根是开方运算的基础，是引入无理数的准备知识．平方根概念的正确理解有助于符号表示的理解，是正确求平方根运算的前提，并且直接影响到二次根式的学习.　算术根的教学不但是本章教学的重点，也是今后数学学习的重点．在后面学习的根式运算中，归根结底是算术根的运算，非算术根也要转化为算术根。　　本节难点是平方根与算术平方根的区别于联系．首先这两个概念容易混淆，而且各自的符号表示意义学生不是很容易区分，教学中要抓住算术平方根式平方根中正的那个，讲清各自符号的意义，区分两种表示的不同.对于平方根运算不仅数　　3.本节主要内容是平方根和算术平方根，注意数字要简单，关键让学生理解概念．另外在文字叙述时注意语言的严谨规范．

算术平方根,平方根的定义

　　算数平方根：如果一个正数的平方等于a，那么这个正数x叫做a的算术平方根，a叫做被开方数　　平方根：如果一个数的平方等于a，那么这个数叫做平方根或二次方根。

编辑本段学生用计算器求平方根教案

教学重点难点分析

　　教学重点是用计算器求一个正数的平方根的程序.无论实际生活，还是其他学科都会经常用到计算器求一个数的平方根，这也是学生的基本技能之一．　　教学难点准确用计算器求一个正数的平方根.由于开平方运算要用到第二功能键，学生容易漏掉此步操作，在教学过程中要着重说明此键的作用功能．(注：sqrt = squareroot平方根)

教法建议

　　在给学生讲解如何利用计算器求一个数的平方时，应掌握方法。

编辑本段计算机科学

用Ruby求平方根

　　module MyMath　　def sqrt(num,rx=1,e=1e-10) #参数1，需要求平方根的目标；参数2，迭代区间；参数3，精度　　num*=1.0 #目标初始化　　(num-rx*rx).abs < e ? rx :sqrt(num,(num/rx+rx)/2,e) #计算平方根　　end　　end　　include MyMath　　puts sqrt(2) #求2的平方根　　puts sqrt(2,5,0.01) #求2的平方根+迭代区间与精度。

C语言版求平方根

　　double Sqrt(double a,double p)//a是被开平方根数，p是所求精度　　{double x=1.0;double cheak;　　do{x=(a/x+x)/2.0;cheak=x*x-a;}while(cheak<-p ||cheak>p);return x;}int main(int argc, char* argv[])　　{printf("%.4fn",Sqrt(2.0,0.0001));//有时输出精度要比所求精度少一位，即%.3f　　printf("%.4fn",Sqrt(0.09,0.0001));　　return 0;}　　输出结果：　　1.4142　　0.3000

平方根表

　　12^2=144 13^2=169 14^2=196 15^2=225 16^2=256 17^2=289 18^2=32419^2=361 20^2=400 21^2=441 22^2=484 23^2=529 24^2=57625^2=625公式X_(n+1)={X_n+[A/X^（k-1）-X_n]1/k}　　公式X_(n+1)={X_n+[A/(X^（k-1）-X_n]1/k}　"_"表示下角标，“^”表示上角标。例如，X^2,表示x的平方；X_1表示第一个X。　　例如，A=5，k=3.　　公式：X(n+1）=Xn+（A/Xn^2-Xn）1/3　　5介于1^3至2^3之间（1的3次方=1，2的3次方=8）　　X_0可以取1.1，1.2，1.3，1.4，1.5，1.6，1.7，1.8，1.9，2.0都可以。例如我们取2.0.按照公式：　　第一步：X_1={2.0+[5/(2.0^2-2.0]1/3=1.7.}。输入值大于输出值，负反馈；　　即5/2×2=1.25，1.25-2=-0.75，0.75×1/3=0.25，　　2-0.25=1.75，取2位数值,即1.7。　　第二步：X_2={1.7+[5/(1.7^2-1.7]1/3=1.71}.。输入值小于输出值，正反馈；　　即5/1.7×1.7=1.73010，1.73-1.7=0.03，0.03×1/3=0.01，　　1.7+0.01=1.71。取3位数，比前面多取一位数。　　第三步：X_3={1.71+[5/(1.71^2-1.71]1/3=1.709}。输入值大于输出值，负反馈　　第四步：X_4={1.709+[5/(1.709^2-1.709]1/3=1.7099}.输入值小于输出值，正反馈；　　这种方法可以自动调节，第一步与第三步取值偏大，但是计算出来以后输出值会自动转小；第二步，第四步输入值偏小，输出值自动转大。X_4=1.7099.　　当然也可以取1.1，1.2，1.3，。。。1.8，1.9中的任何一个。　　开平方公式　　X（n + 1） = Xn + (A / Xn ? Xn)1 / 2.。（n，n+1与是下角标）　　例如，A=5：　　5介于2的平方至3的平方;之间。我们取初始值2.1，2.2，2.3，2.4，2.5，2.6，2.7，2.8，2.9都可以，我们最好取中间值2.5。　　第一步：2.5+（5/2.5-2.5)1/2=2.2；即5/2.5=2，2-2.5=-0.5，-0.5×1/2=-0.25，2.5+(-0.25)=2.25，取2位数2.2。　　第二步：2.2+(5/2.2-2.2)1/2=2.23；　　即5/2.2=2.27272，2.27272-2.2=-0.07272，-0.07272×1/2=-0.03636，2.2+0.03636=2.23。取3位数2.23。　　第三步：2.23+(5/2.23-2.23)1/2=2.236。　　即5/2.23=2.2421525，,2.2421525-2.23=0.0121525，,0.0121525×1/2=0.00607，,2.23+0.006=2.236.，取4位数。　　每一步多取一位数。这个方法又叫反馈开方，即使你输入一个错误的数值，也没有关系，输出值会自动调节，接近准确值，等等。

  
平方根的定义和性质 平方根的性质 

爱华网本文地址 » http://www.aihuau.com/a/25101016/298814.html

更多阅读

律师函的定义及格式 律师函格式

律师函的定义及格式　　律师函，又称律师信，是指律师接受客户的委托就有关事实或法律问题进行披露、评价，进而提出要求以达到一定效果而制作、发送的专业法律文书。　　　1、律师函的本质　　律师函是律师对某一事实进行法律评价和

瘢痕的定义及分类 工业用水分类及定义

瘢痕的定义及分类瘢痕的定义：瘢痕的分类：瘢痕是一个很笼统的概念，它是各种创伤后所引起的正常皮肤组织的外观形态和组织病理学的改变的统称。它是人体创伤（即使是轻微的损伤）后，在伤口或创面自然愈合过程中的一种正常的、必然的生理反应

双曲线定义、标准方程、几何性质 双曲线的简单几何性质

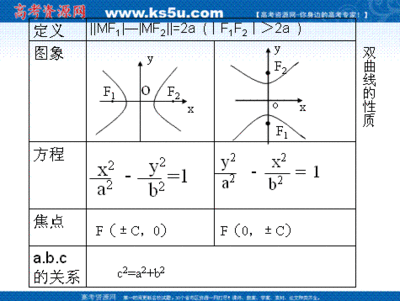
【本讲教育信息】一. 教学内容：双曲线定义、标准方程、几何性质［知识点］（一）双曲线的定义1. （1）图示：取一拉链，在拉开两边上各选一点，分别固定在F1、F2上，|F1F2|＝2c，即|PF1|－|PF2|＝2a，得到的图形，我们称为双曲线一支（加绝对值两支）3. 定义：平面内与两定

容积率的定义及计算 建筑容积率计算公式

容积率，是指一个小区的总建筑面积与用地面积的比率。对于发展商来说，容积率决定地价成本在房屋中占的比例，而对于住户来说，容积率直接涉及到居住的舒适度。一个良好的居住小区，高层住宅容积率应不超过5，多层住宅应不超过2，绿地率应不低

声明:《平方根的定义及性质 平方根性质》为网友谪仙大人分享！如侵犯到您的合法权益请联系我们删除