卢卡斯数列 (Lucas Sequence) 和费波拿契数列 (Fibonnacci Sequence)有莫大的关系。故本人在介绍费波拿契数以後也得为卢卡斯数列多添一章。
【背景】弗朗索瓦·爱德华·阿纳托尔·卢卡斯(François Édouard AnatoleLucas,1842年4月4日-1891年10月3日,法语发音为(IPA)[fʀɑ̃swa eduaʀ anatɔllyka])法国数学家,受教育是在巴黎高等师范。先是在巴黎天文台工作,随后成为一个专业数学家。这期间他曾在陆军服役。卢卡斯的死很不寻常。在法国科学进步协会(Associationfrançaise pour l'avancement desscience)的年度会议的宴会上,一个侍者掉了一个餐盘,其中一个瓷碎片将他的脸划破。过后几天,他就死于可能由败血症引起的严重皮肤感染。卢卡斯以研究斐波那契数列而著名。卢卡斯数列就是以他的名字命名。他曾给出了求斐波那契数列第n项的表达式。卢卡斯创造出检验素数的方法。后来德里克·亨利·莱默完善了他的方法,就是我们用来验证梅森素数的卢卡斯-莱默检验法。他还对休闲数学感兴趣,发明了汉诺塔问题。
先定义整数 P 和Q 使 D = P2 - 4Q > 0,
从而得一方程 x2 - Px + Q = 0,其根为 a, b,
现定义卢卡斯数列为:
Un(P,Q) = (an - bn) / (a-b) 及 Vn(P,Q) = an + bn
其中 n 为非负整数,得 U0(P,Q) = 0、 U1(P,Q) = 1 、 V0(P,Q) = 2 、 V1(P,Q)= P、......
我们有下列和卢卡斯数列相关的恒等式:
Um+n = UmVn - anbnUm-n 、 Vm+n = VmVn - anbnVm-n
Um+1 = P*Um - Q*Um-1 、 Vm+1 = P*Vm - Q*Vm-1 (取 n = 1)
U2n = UnVn 、 V2n = Vn2 - Qn
U2n+1 = Un+1Vn - Qn 、 V2n+1 = Vn+1Vn - PQn
若取 (P,Q) = (1,-1),我们便有 Un 为费波拿契数,
即 0、 1、 1、 2、 3、 5、 8、 13、 21、 34、 55、 89、 144、 233、 377、 610、987、 1597、 2584、 4141、 6765等。
而 Vn 为卢卡斯数 (Lucas Number),
即 2、 1、 3、 4、 7、 11、18、 29、 47、 76、 123、199、 322、 521、 843、 1364、 2207、 3571、 5781、 9349 等。
若取 (P,Q) = (2,-1),我们便有 Un 为佩尔数 (Pell Number),
即 0、 1、 2、 5、 12、 29、 70、 169、 408、 985、 2378、 5741等。
而 Vn 为佩尔 - 卢卡斯数 (Pell - Lucas Number) (详见另文《佩尔数列》),
即 2、 2、 6、 14、 34、 82、 198、 478、 1154、 2786、 6726等。
此等全都是数学界很有名的数列。
卢卡斯数的性质
卢卡斯数 (简记 Ln) 有很多性质和费波拿契数很相似。如 Ln = Ln-1 + Ln-2,其中不同的是 L1 = 1、L2 = 3。
所以卢卡斯数有:1, 3, 4, 7, 11, 18, 29, 47, 76, 123, ...... (OEISA000204),当中的平方数只有 1 和 4,这是由哥恩 (John H. E. Cohn) 证明的。而素数,即卢卡斯素数(Lucas Prime) 则有: 3, 7, 11, 29, 47, ...... 。当中现在知道最大的拟素数 (ProbablePrime) 为 L574219 ,此数达 120005位之多。
我们有下列和卢卡斯数相关的恒等式:
Ln2 - Ln-1Ln+1 = 5 (-1)n
L12 + L22 + ...... + Ln2 = LnLn+1 - 2
Lm+n = (5FmFn + LmLn) / 2 (式中的 Fn 为费波拿契数)
Lm-n = (-1)n (LmLn - 5FmFn) / 2
Ln2 - 5Fn2 = 4 (-1)n
卢卡斯素数龙虎榜
n 数位 发现者 年份
56003 11704 欧文 (Sean A. Irvine) / 禾达 (Bouk de Water) 2006
51169 10694 禾达 (Bouk de Water) / 布靴斯特 (David Broadhurst)
2001
44507 9302 禾达 (Bouk de Water) / 布靴斯特 (David Broadhurst) / 伦斯(John Renze) 2005
36779 7687 禾达 (Bouk de Water) / 布靴斯特 (David Broadhurst) / 伦斯(John Renze) 2005
35449 7409 禾达 (Bouk de Water) 2001
19469 4069 禾达 (Bouk de Water) / 布靴斯特 (David Broadhurst)2002
19449 3020 都伯纳 (Harvey Dubner) / 凯勒 (Wilfrid Keller) 1995
13963 2919 奥基斯 (Mike Oakes) 2002
12251 2561 禾达 (Bouk de Water) / 布靴斯特 (David Broadhurst)2001
10691 2235 都伯纳 (Harvey Dubner) / 凯勒 (Wilfrid Keller) 1995
若我们考虑的是拟素数,即那些通过费马小定理 (Fermat's Little Theorem)逆命题测试的数,这有很大机会是素数,或可能是卡迈克尔数 (Carmichael Number)。那我们可把 n 推至202667。但正因为 n 很大,要判断该数的素性的确不易。
以上所说的就是不仅仅是这些。
联系到当前年中国上证指数如何来看待呢?
如果本轮牛市从05年6月的998点算起,到07年10月6124点。
卢卡斯数字解释:卢卡斯数字和神奇数字系列,都是以加数形式增长.卢卡斯数字是神奇数字的1.328倍,在趋势分析上的应用,和费数大同小异.在时间周期方面,主要是用以数算市场逆转的时间,两套数字序列往往可起互补长短的作用.
本轮牛熊月K线分析
1,998点起头4个月,在千点上下震荡,第1个数字是4,
2,之后连续4根月阳线,7个月后到达1300下方,第2个数字是7,
3,在第11个月后,来到阶段1700下方,然后大盘在此调整震荡,此时上涨幅度近70%,第4个数字是11,
4,在调整4个月后,又开始发力向上,在18个月后大盘冲到2700下方开始震荡调整,第5个数字是18,
5,此后大盘就一鼓作气,在29个月后见顶6124点,到达本轮牛市至高点,此后开始单边下跌,第6个数字是29,
综述及猜想
从01年06月起,到07年10月,时间周期刚好是76个月(4*12个月+4个月),本轮牛市高点离上轮高点整整76个月,这个76也是卢数的又一个数字.而在(三)中也描述了本轮牛市上涨的数字巧合,
下一个卢数是123,对应的时间是2011年09月,离现在还有33个月,会不会是下一波的阶段低点呢?
从07年11月趋势扭转之后,到08年10月18XX点,几乎单边下跌了11个月,(前文已经说过,卢数意味着变盘),11月之后就开始止跌回升,在11这个卢数之后的数字是18,7个月后会不会产生阶段变盘的重要因素呢?也就是09年的6月.在之前巧合(二)里面猜想中,已经提到09年7月会不会是另外一个重要的时间窗口,由于卢数的提前变盘预示,09年6月会不会另外一个重要的变盘转折点?综合近期国内和国际的金融与经济形势,是不是可以得出一个这样的推断,09年第1季度末,就得非常小心谨慎?
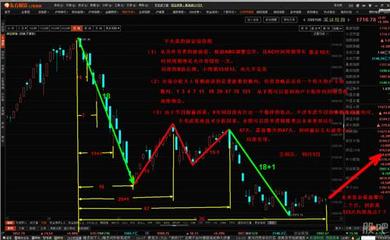
结论:下一轮牛市结束时间为:2011年的9月。
 爱华网
爱华网



