Fourier's law
(傅立叶导热定律,Fourier's law of heatconduction)
傅立叶定律是传热学中的一个基本定律。
可以用来计算热量的传导量。
相关的公式如下
Φ=-λA(dt/dx)
q=-λ(dt/dx)
其中Φ为导热量,单位为W
λ为导热系数
A为传热面积,单位为m^2
t为温度,单位为K
x为在导热面上的坐标,单位为m
q是沿x方向传递的热流密度(严格地说热流密度是矢量,所以q应是热流密度矢量在x方向的分量)单位为W/m^2
dt/dx是物体沿x方向的温度变化率
一般形式的数学表达式:q=-λgradt=-λ(dt/dx)n
式中:gradt是空间某点的温度梯度(temperaturegradient);n是通过该点的等温线上的法向单位矢量,
指温度升高的方向
上述式中负号表示传热方向与温度梯度方向相反
λ表征材料导热性能的物性参数(λ越大,导热性能越好)
第一节 热传导
一、傅立叶定律
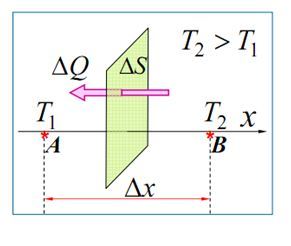
如图4—1所示,热能总是朝温度低的方向传导,而导热速率dQ则和温度梯度 以及垂直热流方向的截面dA成正比:
dQ=- (4—1)
式中负号表示dQ与的方向相反,比例系数 称为导热系数。根据傅立叶定律(4—1)可以导出各种情况下的热传导计算公式。
图4—1 温度梯度与图4—2单层平壁的
热流方向的关系稳定热传导
二、导热系数
导热系数的定义式为:
(4—2)
导热系数在数值上等于单位导热面积、单位温度梯度下在单位时间内传导的热量,这也是导热系数的物理意义。导热系数是反映物质导热能力大小的参数,是物质的物理性质之一。
导热系数一般用实验方法进行测定。通常金属导热系数最大,非金属固体的导热系数较小,液体更小,而气体的导热系数最小。因而,工业上所用的保温材料,就是因为其空隙中有气体,所以其导热系数小,适用与保温隔热。
三、平壁的稳定热传导
(一)(一)单层平壁
如图4—2所示,平壁内的温度只沿垂直于壁面的x方向变化,因此等温面都是垂直于x轴的平面。根据傅立叶定律可由下式求算:
(4—3)
利用上式可解决热传导量(或热损失)Q;保温材料厚度b;外侧温度t;结合热量衡算式可进行材料导热系数λ的测定。
设壁厚x处的温度为t,则可得平壁内的温度分布关系式(4—4),表示平壁距离和等温面t两者的关系为直线关系。
(4—4)
(二) 多层平壁
在稳定导热情况下,通过各层平壁的热速率必定相等,即 Q = Q = 。则通过具有n层的平壁,其热传导量的计算式为:
(4—5)
热阻大的保温层,分配于该层的温度差亦大,即温度与热阻成正比。
四、圆筒壁的稳定热传导
(一)(一)单层圆筒壁
如图4—3所示,圆筒壁的传导面积随半径r在变化,即, 壁两侧温度各为 t、t ,且t >t 。温度沿r方向改变,温度场仍为“一维”。等温面是同轴的园柱面。其热传导的计算式为:
(4—6)
式中 ——圆筒壁的厚度,,m;
——对数平均面积,当时,可用算术平均值。
图4—3 圆筒壁的热传导
设壁厚r处的温度为t,则可得出圆筒壁内的温度分布关系式(4—7),表示圆筒壁距离和等温面温度t两者的关系为对数曲线关系。
(4—7)
(二)(二)多层圆筒壁
多层圆筒壁的导热过程可视为各单层圆筒壁串联进行的导热过程。其计算式可参照多层平壁,对于n层圆筒壁的计算式为:
(4—8)
注意:
(1)上述关于壁的一维稳定热传导的计算问题,虽然有平壁与圆筒壁,单层壁与多层壁之分,但就热传导速率计算公式的形式而言,则是完全相同的,即都可采用一般的公式表示之。
(4—9)
(2)各种情况下热传导的计算式,都是由傅立叶定律积分而得,其关键在热传导的面积。对于平壁,A =A各层面积相等;对圆筒壁A=2 ,A随半径r而变化,故计算式中热传导面积取对数平均面积A ;对空心球壁,A=4 ,算式中热传导面积取几何平均面积.
(3)材料导热系数视为常数,是指工程计算时一般取两侧壁面算术平均温度下的导热系数值。
第二节 传导传热 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
日期:2008-4-5 3:16:21 来源:来自网络 查看:[大 中 小] 作者:不详 热度: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
传导传热也称热传导,简称导热。导热是依靠物质微粒的热振动而实现的。产生导热的必要条件是物体的内部存在温度差,因而热量由高温部分向低温部分传递。热量的传递过程通称热流。发生导热时,沿热流方向上物体各点的温度是不相同的,呈现出一种温度场,对于稳定导热,温度场是稳定温度场,也就是各点的温度不随时间的变化而变化。本课程所讨论的导热,都是在稳定温度场的情况下进行的。 一、传导传热的基本方程式----傅立叶定律 在一质量均匀的平板内,当t1> t2热量以导热方式通过物体,从t1向t2方向传递,如图3-7所示。
取热流方向微分长度dn,在dt的瞬时传递的热量为Q,实验证明,单位时间内通过平板传导的热量与温度梯度和传热面积成正比,即: dQ∝dA·dt/dn 写成等式为: dQ=-λdA·dt/dn(3-2) 二、导热系数λ 导热系数是物质导热性能的标志,是物质的物理性质之一。导热系数λ的值越大,表示其导热性能越好。物质的导热性能,也就是λ数值的大小与物质的组成、结构、密度、温度以及压力等有关。λ的物理意义为:当温度梯度为1K/m时,每秒钟通过1m2的导热面积而传导的热量,其单位为W/m·K或W/m·℃。 表3-1 某些固体在0~100℃时的平均导热系数
三、平面壁稳定热传导 1、单层平面壁
在稳定导热时,导热速率Q不随时间变化,传热面积A和导热系数 λ也是常量,则傅立叶公式可简化为:
2、多层平面壁
设各层壁厚及导热系数分别为b1,b2,b3及λ1,λ2,λ3.内表面温度为t1,外表面温度为t4,中间两分界面的温度分别为t2和t3。
(a)+(b)+(c)有:△t1+△t2+△t3=Q1R1+Q2R2+Q3R3
四、圆筒壁稳定热传导 化工生产中常用的容器、管道一般是圆筒形的,经过圆筒壁的稳定热传导与平面壁的区别在于圆筒壁的内外表面积不等。热流穿过圆筒壁的传热面积不象平面壁那样是固定不变的,而是随圆半径而改变。
圆筒的内半径为r1,外半径为r2,长度为L。若在半径为r处取一微分厚度dr,则传热面积A=2πrL可以看成是常数。由傅立叶定律,通过这一微分厚度dr的圆筒壁的导热速率为:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 爱华网
爱华网