这是OliverWendellHolmes吟咏鹦鹉螺的诗句。鹦鹉螺之吸引诗人,并激起他的丰富的想象,在于螺壳形状的独特:一条等角 螺线,即对数螺线。所谓等角螺线就是向径和切线的交角永远不变的曲线。对数螺线是一根无止尽的螺线,它永远向着极绕,越绕越靠近极,但又永远不能到达极。据说,使用最精密的仪器也看不到一根完全的对数螺线,这种图形只存在数学家的假想中。也许正是这神奇的形状,让苏格兰博物学家和数学家汤普森(D’ArcyThompson,1860~1948)语出惊人:地球上所有动物和植物只有通过数学才能理解!
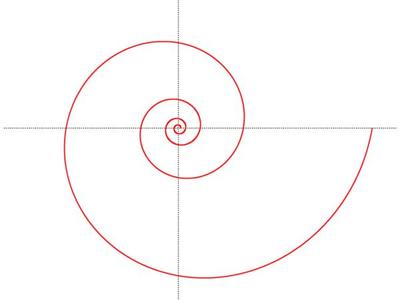
对数螺线在自然界中最为普遍存在,其它螺线也与对数螺线有一定的关系,不过目前我们仍未找到螺线的通式。以后若去动物园可瞧仔细了:象鼻、羊角、鹦鹉的爪子等也都是成等角螺线形的。圆网蛛能织出这种曲线,许许多多贝壳动物身上都有这种曲线。令人惊奇的是,人们在一种中生代化石——菊石上发现了这种漂亮的曲线;鹰以对数螺线的方式接近它们的猎物;昆虫以对数螺线的方式接近光源;用天文望远镜观察到的星云中也有螺线形状的!难怪法布尔会惊叹:“几何,以及面积上的和谐,支配着一切。几何存在于松果鳞片的布置中,也存在与圆网蛛的黏胶丝上;蜗牛的螺旋上升斜线里有几何,蜘蛛网的念珠里有几何,行星轨道里也有几何;几何到处存在,不管在原子世界里还是在无限辽阔的宇宙中,几何都是非常高明的!”
对数螺线是1638年经笛卡尔引进的,后来瑞士数学家雅各.伯努利曾详细研究过它,发现对数螺线的渐屈线和渐伸线仍是对数螺线,极点在对数螺线各点的切线仍是对数螺线,等等。伯努利对这些有趣的性质惊叹不止,竟留下遗嘱要将对数螺线画在自己的墓碑上,并附词“纵使改变,依然故我”(eademmutata resurgo)。可惜雕刻师误将阿基米德螺线刻了上去。
 爱华网
爱华网