※《经济学原理》/{第02篇·市场如何运行}
※《第05章·弹性及其应用》
※{第01节·需求弹性}/专题03
需求价格弹性的计算
需求价格弹性是用需求量变动百分比除以价格变动百分比来计算,即——
需求价格弹性=需求量变动百分比/价格变动百分比
例如:冰淇淋价格上升10%,其购买量减少了20%,那么,冰淇淋的需求价格弹性为:20%/10%=2。即冰淇淋的需求价格弹性是2,表明其需求量变动的比例是其价格变动比例的两倍。
由于一种物品的需求量与其价格呈负相关,所以,数量变动的百分比与价格变动的百分比的符号总是相反的。上例中,价格变动的百分比是正的10%(表明上升),需求量变动的百分比是负的20%(表明减少)。出于这个原因,需求价格弹性有时为负数。但是,也可遵循一般做法,去掉负号,把所有价格弹性表示为正数(即数学上的绝对值)。这样处理后,需求价格弹性越大,意味着需求量对价格越敏感。
一个计算变动百分比和弹性的更好方法——中点法
如果要计算一条需求曲线上两点之间的需求价格弹性,会发现一个问题:从A点到B点的弹性不同于从B点到A点弹性。
例如:A点,价格=4,数量=120;B点,价格=6,数量=80
从A点到B点,价格上升50%,数量减少33%,需求价格弹性是33/50,即0.66;
从B点到A点,价格下降33%,数量增加50%,需求价格弹性是50/33,即1.50 ;
产生这种差别是因为上述变动百分比是根据不同的基础计算的。
那么,避免这个问题的一种方法是用中点法计算弹性。计算变动百分比的标准方法是用变动量除以原来的水平。与之相似,中点法是用变动量除以原来水平与最后水平的中点值(或平均值)来计算变动百分比。
例如:价格从4到6的中点值是5,因此,根据中点法——
价格从4到6是上升了40%,因为,(6-4)/5*100%=40%
价格从6到4是下降了40%,因为,(4-6)/5*100%=40%
即无论变动的方向如何,中点法得出的答案都是相同的,所以,在计算两点之间的需求价格弹性时通常用这种方法。
那么上例中,A点与B点之间的中点是:价格=5,数量=100;根据中点法——
从A点到B点,价格上升40%,数量减少40%;
从B点到A点,价格下降40%,数量增加40%;
在这两种变动方向上,需求价格弹性都等于1。
用中点法计算需求价格弹性的公式
(Q2-Q1)/[(Q2+Q1)/2]
—————————————(注:P代表价格;Q代表数量。)
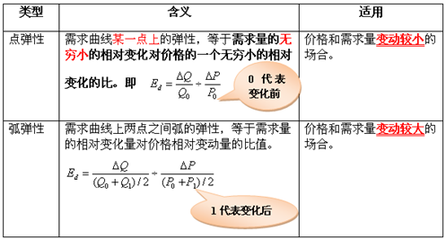
(P2-P1)/[(P2+P1)/2]
 爱华网
爱华网