二叉树中有一种特别的树——哈夫曼树(最优二叉树),其通过某种规则(权值)来构造出一哈夫曼二叉树,在这个二叉树中,只有叶子节点才是有效的数据节点(很重要),其他的非叶子节点是为了构造出哈夫曼而引入的!
哈夫曼编码是一个通过哈夫曼树进行的一种编码,一般情况下,以字符:‘0’与‘1’表示。编码的实现过程很简单,只要实现哈夫曼树,通过遍历哈夫曼树,规定向左子树遍历一个节点编码为“0”,向右遍历一个节点编码为“1”,结束条件就是遍历到叶子节点!因为上面说过:哈夫曼树叶子节点才是有效数据节点!
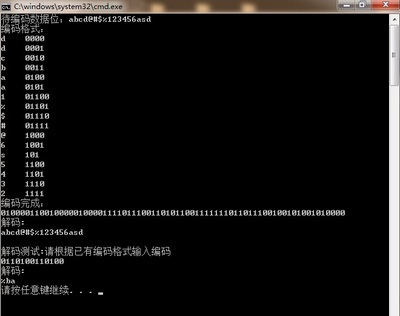
如下图就是一个哈夫曼编码例子程序效果图:
下面就来一步步实现这个过程:
前面已经说关键是构造一棵哈夫曼树,只要构造出了这棵哈夫曼树,编码就很简单,但哈夫曼树的构造是根据实际的情况来构造的,并不是随随便便就构造的!既然是二叉树那么我们首先就定义一个二叉树结构:
structtree
{
char date;//数据
bool min;//叶子节点
int quanzhi;//权值
struct tree *zuo,*you;//左右孩子
}*tre;
其中权值是我们最需要关心的,因为我们就是要通过权值来构造,但权值怎么规定呢?当然是根据实际情况来!其中叶子节点是为了标记是叶子节点,便于后期编码!
为了简单说明,第一个例子就直接定义多个哈夫曼树节点,然后通过这些节点来构造出最终的哈夫曼树!
treetr[9]={{'a',true,5},{'b',true,2},{'c',true,9},{'d',true,3},{'e',true,6}};
tr是一个哈夫曼数组,其中每个元素都是一个哈夫曼树,我们的任务就是将这些元素“整合”起来,使它们联系起来构成一个哈夫曼树。初始时,数组每个元素都是没有联系的,我们的任务就是把它们通过struct tree *zuo,*you;//左右孩子 来连接起来,形象上就是构成一棵二叉树。
我们先通过语言叙述的方法来构造一棵哈夫曼二叉树:
a权值5
b权值2
c权值9
d权值3
e权值6
首先,取权值最小的两个节点“整合”出一个新的节点,该节点的权值为最小两个节点权值之和。如下图:
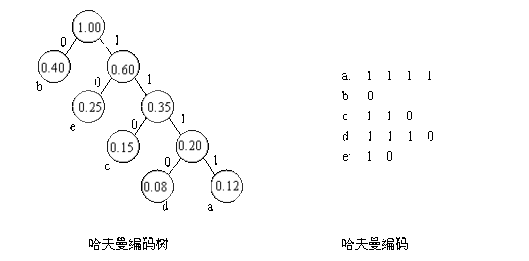
然后,将这个新的节点与剩下元素进行权值比较,依旧取最小的两个权值节点构造 新的节点,反复这个过程,直到取完所有元素,本例的哈夫曼树如下图:
其中叶子节点(也就是2,3,5,6,9)是有效的数据节点!构造时节点的左右顺序并不影响哈
曼树的构造,但会导致出现不同的编码,当然编码只要不出现前缀码就是正确的编码。
实现算法:
实现算法有很多种,关键是要理解它构造的原理。
通过上面的例子,我们知道构造一个哈夫曼树,需要的节点数数有效数据节点的2*n-1,其中
n是有效数据的个数,如上面例子,有效数据个数有5个,但最终构造出的哈夫曼树有2*5-1=9
个节点,所以根据这个性质就可写出一种算法:
treetr[9]={{'a',true,5},{'b',true,2},{'c',true,9},{'d',true,3},{'e',true,6}};
5个数据所以需要9个空间,其中9-5=4个空间是给那些无效节点使用的(哈夫曼树种非叶
子节点)。
首先,我们遍历这个数组,找到最小的两个元素。
然后,将他们移动到前面,并将权值求和构造出新的节点,新的节点左右子树指向最小的两个元素,将这个新节点插入有效数据后面。
最后,从第2+1个元素(前面两个无需遍历了)开始重新遍历。
重复上述过程,直到数组填满,填满后的最后一个元素就是最终的哈夫曼树。
如第一次遍历后数组tr[9]状态就变为:
treetr[9]={ {'d',true,3},{'b',true,2},{'c',true,9},{'a',true,5},{'e',true,6},{‘’,false,5,tr[0],tr[1]}}
最小的两个元素移到了前面,有效数据增加了一个,并且新节点左右子树指向前面两个元素。
完整哈夫曼实现代码如下;
// hfm.cpp: 定义控制台应用程序的入口点。
//
#include"stdafx.h"
#include
////////////贵州民族大学///////////////
///////////编译环境vs2010//////////////
static inthfmb=0;
structtree
{
char date;//数据
bool min;//叶子节点
int quanzhi;//权值
struct tree *zuo,*you;//左右孩子
}*tre;
structshfm
{
char date;//字符数据
char bianm[11];//哈夫曼编码,最大编码数为11(可根据实际修改!)
}hfm[100];//哈夫曼编码对应真实数据表
voidgettree(tree tr[],int shij,int youx)//构造哈夫曼树,tr树集合,shij集合实际数据个数,youx集合有效数据个数
{
//模拟动态增长数组,每次构造新的树就插入有效数据后面
if (2*youx-1!=shij)
{
printf("参数不符合!");
return;
}
int c=0;
while(youx!=shij)//当有效个数==实际个数时,构造完成!
{
for (int i=c;i
{
//每次循环取两个最小值并将两个最小值放置在当前循环起始两位
if (tr[i].quanzhi
{
tree p=tr[i];
tr[i]=tr[c];
tr[c]=p;
}
if (tr[i].quanzhi
{
tree p=tr[i];
tr[i]=tr[c+1];
tr[c+1]=p;
}
}
//以下为通过最小值构造的新树
tr[youx].quanzhi=tr[c].quanzhi+tr[c+1].quanzhi;
tr[youx].you=&tr[c];//新树右孩子指向当前循环的最小值之一
tr[youx].zuo=&tr[c+1];//新树左孩子指向当前循环的最小值之一
youx++;//新树插入当前有效数据个数后面并使有效数据个数+1
c=c+2;
}
}
voidbianltree(tree *tr,char ch[])//哈夫曼编码
{
//通过遍历树,得到每个节点的编码
static int i=0;
if (!tr->min)//叶子节点
{
ch[i]='0';
i++;
bianltree(tr->zuo,ch);//左节点编码为"0"
ch[i]='1';
i++;
bianltree(tr->you,ch);//右节点编码为"1"
}
if (tr->min)
{
ch[i]='�';//结束标记()
printf("%c %sn",tr->date,ch);
hfm[hfmb].date=tr->date;
int j=0;
while(j!=i||i>10)
{
hfm[hfmb].bianm[j]=ch[j];
j++;
}//保存编码映射表
hfmb++;
}
i--;//递归走入右叶子节点时,取消当前赋值(当前必为左边叶子节点)
}
int_tmain(int argc, _TCHAR* argv[])
{
treetr[9]={{'a',true,5},{'b',true,2},{'c',true,9},{'d',true,3},{'e',true,6}};
//printf("%dn",sizeof(tr)/sizeof(tree));
gettree(tr,9,5);
char ch[100];
//printf("%sn",ch);
bianltree(&tr[8],ch);
return 0;
}
效果:
其中gettree()函数是构造哈夫曼过程,bianltree()是通过哈夫曼树编码过程,struct shfm
结构体是保存字符数据与它的哈夫曼编码的映射表,可用也可不用,这里之所以使用,是因为通过一次遍历就可得到所有元素的编码,以后要编码只需查表即可,以空间换时间。
下面介绍哈夫曼的应用举例:
通过上文的介绍,下面就介绍哈夫曼的实际运用。
本例的模拟效果是:通过传入一串字符串,返回该字符串的编码。并且通过传入一个有效的编码得到一个字符串!
下面给出完整代码,该代码基于上述代码之上进行修改,并优化上述代码。
// hfm.cpp: 定义控制台应用程序的入口点。
//
#include"stdafx.h"
#include
////////////贵州民族大学///////////////
///////////编译环境vs2010//////////////
static inthfmb=0;
structtree
{
char date;//数据
bool min;//叶子节点
int quanzhi;//权值
struct tree *zuo,*you;//左右孩子
}*tre;
structshfm
{
char date;//字符数据
int len;//编码长度
char bianm[11];//哈夫曼编码,最大编码数为11(可根据实际修改!)
}hfm[100];//哈夫曼编码对应真实数据表
voidgettree(tree tr[],int shij,int youx)//构造哈夫曼树,tr树集合,shij集合实际数据个数,youx集合有效数据个数
{
//模拟动态增长数组,每次构造新的树就插入有效数据后面
if (2*youx-1!=shij)
{
printf("参数不符合!");
return;
}
int c=0;
while(youx!=shij)//当有效个数==实际个数时,构造完成!
{
for (int i=c;i
{
//每次循环取两个最小值并将两个最小值放置在当前循环起始两位
if (tr[i].quanzhi
{
tree p=tr[i];
tr[i]=tr[c];
tr[c]=p;
}
if (tr[i].quanzhi
{
tree p=tr[i];
tr[i]=tr[c+1];
tr[c+1]=p;
}
}
//以下为通过最小值构造的新树
tr[youx].quanzhi=tr[c].quanzhi+tr[c+1].quanzhi;
tr[youx].you=&tr[c];//新树右孩子指向当前循环的最小值之一
tr[youx].zuo=&tr[c+1];//新树左孩子指向当前循环的最小值之一
youx++;//新树插入当前有效数据个数后面并使有效数据个数+1
c=c+2;
}
return ;
}
voidbianltree(tree *tr)//哈夫曼编码
{
//通过遍历树,得到每个节点的编码
static char ch[100];
static int i=0;
if (!tr->min)//叶子节点
{
ch[i]='0';
i++;
bianltree(tr->zuo);//左节点编码为"0"
ch[i]='1';
i++;
bianltree(tr->you);//右节点编码为"1"
}
if (tr->min)
{
ch[i]='�';//结束标记()
printf("%c %sn",tr->date,ch);
hfm[hfmb].date=tr->date;
hfm[hfmb].len=i;
int j=0;
while(j!=i||i>10)
{
hfm[hfmb].bianm[j]=ch[j];
j++;
}//保存编码映射表
hfmb++;
}
i--;//递归走入右节点时,取消当前赋值(当前必为左边叶子节点)
}
voidchushihuahmf(tree *hfmtree,char *str,int i)
{//初始化哈夫曼树数组!参数:含哈夫曼树数组,待编码数据串,数据串长度
int j=0;
while(*str)
{//初始化有效的数组元素
hfmtree->date=*str;//待编码数据
hfmtree->min=true;//是否叶子节点
hfmtree->quanzhi=*str;//权值
str++;
hfmtree++;
j++;
}
while(j<=2*i-2)
{
//初始化非有效数组元素
hfmtree->min=false;//全部非叶子节点
j++;
hfmtree++;
}
//注:本函数权值是根据字符ascll码判断!可根据实际情况重新定义初始化函数!
}
char *hfmbm(char *str)
{//哈夫曼编码函数 参数:待编码字符串!
int i=0;//统计字符串字符数
int j=i;
char *p=str;//备份字符串首地址
while(*str)//统计字符数
{
i++;
str++;
}
//printf("%d",i);
tree *hfmtree=(tree*)malloc(sizeof(tree)*(2*i-1));//根据字符数开辟可用空间
str=p;
tree *pp=hfmtree;//备份哈夫曼数组首地址
chushihuahmf(hfmtree,str,i);//根据ascll码制定权值并依此构造数组(根据实际情况可自行修改)
hfmtree=pp;
gettree(hfmtree,2*i-1,i);//构造一个哈夫曼树
tre=&hfmtree[2*i-2];//得到哈夫曼树
bianltree(tre);//通过哈夫曼树编码并保存在编码
char *restr=(char *)malloc(sizeof(char)*i*11);//开辟编码后的字符串地址
int k=0;
p=restr;
while(k
{//通过遍历编码映射表 编码字符 通过映射表的字符匹配后返回编码
int b=0;
while(b
{
if (hfm[b].date==str[k])
{
for (int j=0;j
{
*restr=hfm[b].bianm[j];
restr++;
}
break;
}
b++;
}
k++;
}
*restr='�';
restr=p;
printf("编码完成:n%sn",restr);
return restr;
}
voidhfmjm(char *hmf)
{//哈夫曼解码参数哈夫曼编码后的数据串
tree *p=tre;//得到哈夫曼树
while(*hmf)
{
if (*hmf=='0')//编码为0走左子树
{
tre=tre->zuo;
if (tre->min)//为叶子节点
{
printf("%c",tre->date);//输出编码
tre=p;
}
hmf++;
continue;
}
if (*hmf=='1')//编码为1走右子树
{
tre=tre->you;
if (tre->min)
{
printf("%c",tre->date);
tre=p;
}
hmf++;
continue;
}
printf("不能识别编码:%cn",*hmf);
return;
}
printf("n");
tre=p;//还原哈夫曼树
//注:本解码是根据哈夫曼树解码本程序还可以根据编码映射表解码
}
int_tmain(int argc, _TCHAR* argv[])
{
char *ch="abcd@#$3456asd";
printf("待编码数据位:%sn",ch);
printf("编码格式:n");
char *str=hfmbm(ch);
printf("解码:n");
hfmjm(str);
//////解码测试:只要输入编码映射表(struct shmf结构体)有的编码就能实现解码!
printf("n解码测试:请根据已有编码格式输入编码n");
char hmf[100];
gets(hmf);
printf("解码:n");
hfmjm(hmf);
return 0;
}
测试效果1:
测试效果2:
函数说明:
char *hfmbm(char *str)函数是完成哈夫曼树构造的函数,用户只需传入一个带编码的字符串就可,本函数就可根据字符串开辟数组空间,并构造哈夫曼树。
voidchushihuahmf(tree *hfmtree,char *str,int i)函数是初始化哈夫曼树权值的函数,因为我们构造时需要指定构造规则(即权值),本函数为了方便,直接使用ascll码作为权值构造,本函数可根据实际情况修改。
voidhfmjm(char *hmf)函数是解码函数,通过传入有效编码解码出字符串!
从效果图中,我们发现相同元素有不同的编码,不过这不影响编码与解码,但从空间、时间角度应该避免这种情况,篇幅有效,本文将不再处理,在本例中由于有映射表,所有可以通过遍历映射表删除重复元素。
 爱华网
爱华网