现代资产组合管理理论是20世纪50年代由美国的一位大学教授哈里·马柯维茨(Harry·Markowitz)在1952年发表的论文《资产组合选择》中首先提出并发展起来。他第一次运用方差和期望值作为对风险和收益的度量,奠定了现代风险分析的基础。
马柯维茨从投资者的资产选择为出发点,指出了风险和收益的权衡关系,从理论上推导出最优的投资组合,并提出了一系列重要概念。这些内容已逐渐发展成为主流的风险与收益理论。成为现代投资学产生的重要标志。
现代资产组合理论的基本前提是:
投资者都是厌恶风险的(风险规避型。一项资产的风险越大,该资产就越没有吸引力)
,投资者只根据期望收益率和标准差两个指标进行投资判断。因此,在标准差相同时,
投资者会选择期望收益率最高的资产。
1、可行集与有效集(有效边界、效率边界)
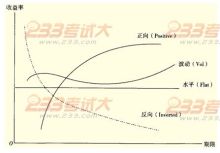
由N个资产构成的投资组合,由于权重不同可以有无穷多个可能的组合,这些组合称为可行集合(或可行投资组合)。见P.85,图6-6为预期收益率---标准差(或均值—方差)的图形中的伞形区域。
风险相同情况下预期收益最高和预期收益相同情况下风险最小的投资组合称为有效集合(有效边界或有效投资组合)。
2、投资者的效用函数与无差异曲线
投资者在有效边界中选取何种组合,取决于投资者对收益与风险的权衡态度,即投资者的主观偏好,可用效用函数来表示。不同的投资者有不同的效用函数。
将对投资者具有同样效用的资产组合形成一条曲线,就是无差异曲线。它表示:投资者认为同样满意的那些不同风险和收益率的搭配。
在均值——方差图上,风险偏好投资者的无差异曲线平缓,风险厌恶投资者的无差异曲线陡峭。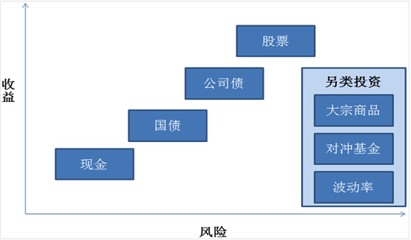
无差异曲线与纵轴的交点的收益率代表无风险资产的收益率。
无差异曲线的位置越高,曲线上组合的满意程度越高。
3、最优投资组合与无风险资产
确定投资组合的有效边界后,投资者利用无差异曲线就可以在有效边界上选出满足个人偏好的投资组合。
由于无差异曲线的位置越高,曲线上组合的满意程度越高。因此,有效边界上位于最靠上的无差异曲线上的投资组合是投资者看来最优投资组合(OptimalPortfolio).上述最优投资组合中的资产都是风险资产。而无风险资产也应纳入投资组合选择。
无风险资产是指收益率确定的资产,相应地,无风险利率就是确定的收益率。也就是说,无风险资产的收益率不受任何因素的影响,因此,它与风险资产的协方差为0。风险资产与无风险资产组成的投资组合,,它的期望值和标准差都同风险资产的相应值呈线形关系。
无风险资产的存在,扩大了风险资产的有效边界。投资者的有效边界扩大到过(0,风险收益率)和原风险资产有效边界切点的一条直线上,这条线被称作资本市场线(CML)。
投资者通过借贷,选择在资本市场线上的某一点投资。这一点成为投资者最满意的投资组合。
二、资本资产定价模型——风险与收益理论
资本资产定价模型(CAPM,Capital Asset PricingModel)是在现代投资组合理论基础上发展起来的。由William Sharp等人在1960年代提出。
CAPM假定:所有投资者按马氏的资产选择理论投资;对期望收益与方差和协方差等的估计相同;投资人可以自由借贷。
基于这些假设,资本资产定价模型研究在市场均衡的条件下,预期收益率和风险的关系。
CAPM表示为:
Rj=Rf+(Rm-Rf)*β
式中:
Ri——第i个种证券的预期收益率;
RM——市场资产组合的预期收益率 ;
Rf——无风险资产收益率;
RM- Rf——市场资产组合的风险溢价
β——贝塔系数。第i种证券的收益变动相对于证券市场收益变动的反应程度。
CAPM说明:
1、单个证券的收益率高低决定于2部分:无风险收益率和对所承担的风险的补偿——风险溢价(风险收益、风险升水)。
其中,风险溢价=该资产(证券)的预期收益率-无风险收益率
即: Ri - Rf = 该资产的β×(市场组合预期收益率-无风险收益率)所以:CAPM说明了资产的风险收益率的高低。
2、风险溢价的大小取决于贝塔值的大小,贝塔值越大,表明单个证券的风险越高,所得的补偿也就越高。CAPM表明:风险与收益之间的线性关系——单个证券的预期收益率与其贝塔系数线性相关。
3、贝塔值度量的是单个证券的系统性风险,非系统性风险没有风险补偿。
因为,充分多样化资产组合的风险完全来自该资产组合中资产的系统
性风险,我们只关心某项证券的系统性风险。
一项资产的系统性风险用贝塔的概念来衡量。或者说,贝塔是衡量某项
资产的收益对整个资本市场收益变动敏感性的指标。
例如:当市场资产组合的收益平均上升1%,导致某项证券的收益上升2%
时,则该项证券的贝塔值是2.0;相反,如果市场收益上升1%,某项证券的收
益上升0.5%时,则该项证券的贝塔值为0.5.
贝塔值为2.0的证券的系统性风险大于贝塔值为0.5的证券;当市场收益
发生变动时,贝塔值为2.0的证券的波动2倍于市场收益的波动;它的收益率
风险为系统性风险的2倍。相反,贝塔值为0.5的证券的波动小于市场,故系
统性风险也较小。
一项证券的贝塔值越大,该资产的系统性风险越大。
CAPM方程式给出了常识性的结论:即:
(1)如果一项资产的贝塔值为0,则表明它没有系统性风险,其风险升水为0;
(2)如果贝塔值为1,则表明该项资产的系统性风险与整个市场相同,其风险收益与市场一致,为(RM-Rf );
(3)如果贝塔值大于1,则其风险升水也高于市场。
比如,假如整个市场的预期收益率为8%,无风险收益率为2%,则市场的风险升水为6%,而贝塔值为2的证券,其表明该项资产的系统性风险与整个市场相同,其风险收益率预计为12%(=2× 6%)。
 爱华网
爱华网