解析函数、处处连续处处不可导函数

如果函数f(z)在及的令域内处处可导，那么称f(z)在解析，如果f(z)在区域D内每一个点都解析，称f(z)是在D内的解析函数。如果f(z)在不解析（不可导）称为f(z)的奇点。和实变函数一样，并不是任何函数的导数存在。下面介绍导数存在的条件。

analytic function

区域上处处可微分的复函数。17世纪，L.欧拉和J.leR.达朗贝尔在研究水力学时已发现平面不可压缩流体的无旋场的势函数Φ（x，y)与流函数Ψ（x，y)有连续的偏导数，且满足微分方程组，并指出f（z）＝Φ（x，y）＋iΨ（x，y）是可微函数，这一命题的逆命题也成立。柯西把区域上处处可微的复函数称为单演函数，后人又把它们称为全纯函数、解析函数。B.黎曼从这一定义出发对复函数的微分作了深入的研究，后来，就把上述的偏微分方程组称为柯西-黎曼方程，或柯西-黎曼条件。K.魏尔斯特拉斯将一个在圆盘上收敛的幂级数的和函数称为解析函数，而区域上的解析函数是指在区域内每一小圆邻域上都能表成幂级数的和的函数。关于解析函数的不同定义在20世纪初被证明是等价的。基于魏尔斯特拉斯的定义，区域上的解析函数可以看作是其内任一小圆邻域上幂级数的解析开拓，关于解析开拓的一般定义是，f（z）与g（z）分别是D与D*上的解析函数，若DÉD*，且在D*上f（z）＝g（z）。则称f（z）是g（z）由D*到D的解析开拓。解析开拓的概念可以推广到这样的情形：f（z）与g（z)分别是两个圆盘D1与D2上的幂级数，且D1∩D2≠，在D1∩D2上f（z)＝g（z )则也称f与g互为解析开拓，把可以互为解析开拓的（f（z），Δ）的解析圆盘Δ全连起来，作成一个链。它们的并记作Ω，得到了Ω上的一个解析函数，称它为魏尔斯特拉斯的完全解析函数，这里可能出现这样的情形，在连成一个链的圆盘中，有一些圆盘重叠在一起，但在这些重叠圆盘的每一个上的解析函数都是不一样的，它们的每一个都称为完全解析函数的分支。这样的完全解析函数实际是一个多值函数。黎曼提出将多值解析函数中的那些重叠的圆盘看作是不同的“叶”，不使他们在求并的过程中只留下一个代表，于是形成了一种称为黎曼面的几何模型。将多值函数看作是定义于其黎曼曲面上的解析函数，这样多值解析函数变成了单值解析函数。

魏尔斯特拉斯以其富有独创性的方法，首次以不依赖于几何直观的严格方式阐述和论证了复变函数论，使这一19世纪中成就最辉煌的数学分支进入了深入发展的阶段．他在这方面的工作不仅见诸论文[2，3，4，5]，而且更多体现在他讲授的课程中[12，15，18]．

　　解析性、解析开拓与完全解析函数

　　魏尔斯特拉斯研究解析函数的出发点是解析性概念．如果定义于复平面的区域D中的复值函数f在D的每个点的一个邻域内可展开为幂级数，则称f在D内解析．这样的函数在复意义下可导．他得到不恒等于零的解析函数f在其零点a处的分解式

f(z)=(z-a)ⁿg(z)，

　　其中g在a的邻域内解析且g(a)≠0．由此得到零点的孤立性和解析函数的唯一性定理．

　　他指出，给定以a为中心、收敛半径为r(>0)的幂级数f，对圆盘|z-a|<r中的每点b，f可展开为以b为中心、收敛半径r(b)≥r-|b-a|的幂级数．由此可按r(b)>r-|b-a|或r(b)=r-|b-a|把收敛圆盘边界上的点分为正则点和奇点两类．前一情形可对f进行解析开拓，后一情形则不能．他证明ρ=inf｛r(b)：|b-a|＜r｝＝0，从而得到幂级数收整数且满足ab≥10)表明此边界可能只含有奇点，他称之为“自然边界”；此时f不可能解析开拓到收敛圆外．

　　这样的开拓可能导致回到同一点时得到不同的函数值．在1884—1885学年的讲授中，魏尔斯特拉斯引进了“解析函数元素”概念．如果S是以a为中心的具有正收敛半径的幂级数，则称(a，S)为一个解析函数元素，简称元素．给定两个元素(a，S)，(b，T)，如果S与T的收敛圆盘之交非空且S与T在此交上相等，则称这两个元素互为直接解析开拓．设(a₀，S₀)，(a₁，S₁)，…，(a_n，S_n)是一个元素链，如果链中任何两个相邻元素互为直接解析开拓，则称(a₀，S₀)与(a_n，S_n)互为解析开拓．从一个元素出发进行一切可能的解析开拓所得到的元素的全体，就是一个整体解析函数，它一般是多值的．这种函数被称为完全解析函数．

　　整函数与亚纯函数

　　魏尔斯特拉斯把只在无穷远点处有一个奇点的解析函数称为整函数，并得到了被R．奈望林纳(Nevanlinna)称为“现代分析中最奇妙的结果之一”的整函数分解为素因子的定

　　在任一|z|≤R上一致收敛，于是整函数

　　其中g是整函数．

　　对于解析函数的孤立奇点，魏尔斯特拉斯区别了极点和本性奇点．在1874年12月16日致科瓦列夫斯卡娅的信^[21]中，他表述了下述命题：如果a是f(z)的本性奇点，则对任何复数c(可为∞)，存在z_n→a，使得f(zn)→c．根据F．卡索拉蒂(Casorati)1864年在柏林游学时所作的笔记，在当时他与魏尔斯特拉斯等人的多次讨论中，已谈到这一定理．卡索拉蒂和Ю．B．索霍茨基(Сохопкий)于1868年分别发表了类似结果．这一定理以及E．皮卡(Picard)于1879年发表的著名定理，成为现代亚纯函数值分布论的起点．魏尔斯特拉斯还得到了具有有限个本性奇点和任意多个(可为无穷个)极点的解析函数的一般表示式．

　　多复变函数论

　　在魏尔斯特拉斯的早期论文中，已引进多复变量幂级数

　　与复n维空间中的一些拓扑概念，定义了多复变量幂级数的收敛多圆柱，他还通过系数估计得到由幂级数表示的函数

g_μ(z₁，…，z_n)=0(μ=1，…，m；m＜n)

　　所确定的隐函数z_v=h_v(z_m+1，…，z_n)(v=1，…，m)可展开为幂级数的定理．

　　魏尔斯特拉斯对多复变函数论的最大贡献，是他于1860年讲课中提出并于1879年发表的“预备定理”[9]：如果F(z₁，…，z_n)是原点邻域内的解析函数，F(0，0，…，0)=0，F(0，…，0，z_n)0，则在原点邻域中F可表示为

　　其中k是不小于1的整数，a_v(z₁，…，z_n-1)(v=1，…，k)在原点邻域内解析且在原点处取零值，g在原点邻域内解析且不等于零．这是多复变函数论中最早的一条深刻定理，它使得现代解析集的局部研究中应用代数方法成为可能，对解析集研究具有重要意义．

　　魏尔斯特拉斯的函数论

　　魏尔斯特拉斯与柯西、黎曼同为复变函数论的奠基人，但在方法与途径上并不相同[11]．他建立解析函数论的原意是作为他关于阿贝尔积分与阿贝尔函数一般理论的导引．现在看来，他的主要目标反倒退居次要地位，而他的严格的、批判的、犀利的观念，以及他所提供的一般性理论和方法，则成为他对这一领域的主要贡献．在这方面，他与黎曼明显不同．黎曼以狄利克雷原理为基础建立他的著名的映射定理，而魏尔斯特拉斯对狄利克雷原理的批评使这个原理和黎曼强有力的方法几乎一蹶不振．直到1899年，希尔伯特的工作才使它们得以“复活”．在谈到黎曼面时，魏尔斯特拉斯说他“不能接受这是函数论真正基础”的提法，虽然他也承认这种方法“具有数学想象力”^[15]．在一般方法论上，他说：“我越是思考函数论——这是我不断研究的领域——的各种原理，就越确信它必须建立在简单的代数真理的基础上；谁如果不是把它建立于简单而基本的代数命题，而是借助于‘直觉’(我用这个词来概括描述)，谁就走上了歧路，不管乍一看它多么有吸引力，例如黎曼那样，他通过这种方法发现了代数函数那么多重要的性质．”不过他也强调在研究时可以采用多种渠道，他讲的“只是关于应当怎样建立系统的理论基础问题”．

　　克莱因在比较这两位数学家时说过：“黎曼具有非凡的直观能力，他的理解天才胜过所有同代数学家．……魏尔斯特拉斯主要是一位逻辑学者，他缓慢地、系统地逐步前进．在他工作的分支中，他力图达到确定的形式．”H．庞加莱(Poincaré)写道，魏尔斯特拉斯使“整个解析函数论成为幂级数理论的一系列推论，因而它就被建立在牢靠的算术基础上”，“黎曼的方法首先是一种发现的方法，而魏尔斯特拉斯的则首先是一种证明的方法”．

　　到19世纪末，德文“Funktionenlehre”几乎已成为按照魏尔斯特拉斯的观念建立的复变函数论的同义词，但也有人持有异议．S．李(Lie)批评德国没有象样的几何学家，他把这种状况归咎于魏尔斯特拉斯学派占据统治地位．克莱因在肯定算术化同时也强调数学决不会由逻辑推导完成，直观总是具有特殊重要性．康托尔甚至提出人们应当区别魏尔斯特拉斯实际所做的工作与围绕着他树立起来的神话．

凡解析函數皆屬光滑函數。解析函數的和、積與合成仍是解析函數（惟合成時須留意定義域的問題）。若解析函數在一個開集上非零，則它在該開集上的倒數仍為解析函數。

解析函数指的是处处可导的函数，它是复变函数论中的主要研究对象。瑞士数学家欧拉于1737年在前人确信负数可以开平方的基础上，用i表示负1的平方根，进而人们引入的虚数的概念，使得实数进一步得到发展，产生了复数与复变量。高斯于1811年正式引入复变函数的概念，柯西提出了解析函数的概念并给出了C.R条件，与1814年建立其复变函数的积分理论，复级数理论是威尔斯特拉斯于19世纪建立的，罗巴切夫斯基与黎曼对复变函数的几何理论作有重大贡献。

解析函数指在复平面上某点邻域内可导，且满足柯西黎曼方程。

所谓解析就是在某个领域内可导，为什么解析函数的导数依旧解析而可导函数的导数不一定可导？

导数通常有两个定义,解析函数的导数是指一个复数,而微积分中的多元函数的导数是指一个线性变换.回想一下,一个R2到R2的多元函数的全微分由四个实数表示,而解析函数却只用两个,就是导数的实部和虚部.

你可以把一个复数等效成一个二维空间的场，然后在里面的积分可以表示功，势能什么的，

以复数作为自变量的函数叫做复变函数,而以复数域上的解析函数为主要研究对象的数学分支就是复变函数论

Fourier变换是属于积分变换的内容
复变函数主要由Cauchy积分理论、Weierstrass级数理论和几何理论三部分组成，和高等数学的部分内容相似，比较容易

复变函数主要是用在电气工程专业的，当然也涉及到通信专业...你学这些专业都会学复变函数的，例如通信，通过傅氏变换可以把其他得信号变成余（正）弦信号...有时还得用拉普拉斯变换....在数学方面也还可以，例如用拉普拉斯求解常微分方程就很简单...对于积分那就更不要说了...把留数和柯西用好了，那简直事半功倍，可以这么说像自动化、通信....这些专业你想把他学好.

大多数的物理问题在实函数的范围内可以得到准确的描述了。但是如果使用复变函数。问题会变得简单。你如果知道复变函数中的留数定理就明白了。实函数下一个积分需要计算半天。使用留数定理只需要你看一眼就可以了。

复变函数在描述波动，描述交流电。描述原子结构中都具有很大的优越性。

复变函数的可微性与解析性有何异同

复变函数试卷上的积分是不是都可以用留数来做？基本上可以。但有些用柯西积分公式简单些。

可微也就是可导。
在一点处解析可推出可微.反之不成立。
在区域上解析等价于可微.

没有对复变函数定义过偏导数，因为没意义。

对于复变函数只有能不能解析的问题。

首先这里没有偏导的说法，左右两边都是关于x的函数

另外求导后两边也是一样的阿

欧拉公式EXP（iX）＝cosX＋isinX实际上是变量X的复值函数，也就是所EXP（iX）是一元实变复值函数。

在专门的复变函数课本上，有推广的欧拉公式：
EXP（iZ）＝cosZ＋isinZ ，这里Z是复平面上任意一点。
函数EXP（iZ）是解析函数，可以对变量Z求导数（就像实变函数一样求导）。
在复变函数理论中
d（sinZ）/dZ＝－cosZ ，d（cosZ）/dZ＝sinZ
而d（EXP（iZ））/dZ ＝i*EXP（iZ）=sinZ－icosZ
所以d（cosZ＋isinZ）/dZ＝sinZ－icosZ
所以d（EXP（iZ））/dZ =d（cosZ＋isinZ）/dZ是成立的。

EXP（iX）＝cosX＋isinX若看成 EXP（iZ）＝cosZ＋isinZ
在Z=X+i·0=X 即点（X，0）处的值
则
[d（EXP（iZ））/dZ ] |z=x＝[d（cosZ＋isinZ）/dZ] |z=x
就是i·EXP（iX）＝sinX－icosX

在某点上连续、解析、可导各有什么区别？

根据导数的定义:
f'(z)=lim(△z→0)（f（z+△z）-f（z））/（△z）=lim(△z→0）((x+△x)²-(y+△y)i-x²+yi)/(△x+△yi)=lim(△z→0)(△x²+2x△x-△yi)/(△x+△yi)
当x=-1/2时，原式=lim(△z→0)(△x²-△x-△yi)/(△x+△yi)
将△z=△x+△yi，因此△x=(△z+△z*)/2,带入原式得：
f'(z)=-1
当x≠-1/2时，若z+△z沿着平行于x轴的直线趋向于z，则△y=0，因此原式=2x，不是定值，因此极限不存在。
因此函数f(z)=x²-iy在直线x=-1/2上可导，在复平面内处处不解析。
用这种方法可以直接判断出可导点的导数值，但是判断起来要比利用C—R方程要复杂得多。

对于复变函数在某点连续、解析、可导的关系如下：
f(z)在z0解析→f(z)在z0连续
↓
f(z)在z0可导→f(z)在z0连续
所有箭头方向都不可逆
而若是在区域D内则
f(z)在D内解析→f(z)在z0解析（z0在D内）
↑↓
f(z)在D得可导→f(z)在z0可导

首先要明确解析函数这个概念，他是对所有可以解析的函数的统称。

那么判断一个函数是否是常函数，有以下几个方面着手：
1，明确一个解析式如 f（x）=a，a是一个常数，那么就可以说这个函数是常函数
2，如果一个函数的导函数恒等于0，那么这个函数也是常函数。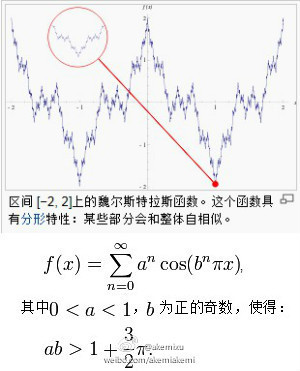

3，任何一个复杂的式子，在通过化简等途径变成了最后的一个确定的值，当然要注意定义域，比如f（x）=lnx+ln(2/x)
当然可能还有更多方面去说明一个函数是常函数，我就抛砖引玉，希望以上所述派的上用场了。

留数(又称残数)　　residue

　　解析函数f（z）沿一条正向简单闭曲线的积分值。严格定义是：f（z）在0＜｜z－a｜≤R上解析，即a是f（z）的孤立奇点，则称积分值（1／2πi）∫｜z－a｜＝Rf（z）dz为f（z）关于a点的留数，记作Res[f（z），a]。如果f（z）是平面流速场的复速度，而a是它的旋源点（即旋涡中心或源汇中心），则积分∫｜z－a｜＝Rf（z）dz表示旋源的强度——环流量，所以留数是环流量除以2πi的值。由于解析函数在孤立奇点附近可以展成罗朗级数：f（z）＝∑ak（z－a）k，将它沿｜z－a｜＝R逐项积分，立即可见Res[f(z)，a]＝a-1，这表明留数是解析函数在孤立奇点的罗朗展式中负一次幂项的系数。

　　关于在扩充复平面上仅有有限多个孤立奇点的解析函数有两条与留数有关的重要性质：①该解析函数沿某一条不过孤立奇点的简单闭曲线积分等于其在曲线内部全部孤立奇点的留数之总和乘以2πi。②该解析函数关于全部孤立奇点的留数之总和为零。这两条性质正好与环流量的可叠加性及质量守恒定律相一致。

　　利用留数的性质以及它与积分的关系,我们可以通过将积分运算转化为留数的计算.

保形映射（conformal mapping）　　解析函数所确定的映射是保形映射。它是复变函数论中最重要的概念之一，与中的概念物理学有联系，而且对物理学中许多领域有重要的应用，例如，应用保形映射成功地解决了流体力学与空气动力学，弹性力学，磁场，电场与热场理论以及其他方面的许多实际问题。不但如此，20世纪中亚音速及超音速飞机的研制促成了从保形映射理论到拟保行映射理论的发展。

　　又称保形映照。解析函数实现的映射有许多重要性质，如“解析函数将区域映射为区域”，“解析函数在其导数不为零的点的邻域内映射是双方单值的。”但最重要的映射特征是：双方单值的解析映射一定是保形映射。

满足条件

　　所谓保形映射是指满足以下两个条件的映射：①过一定点的曲线的正向切线到其象曲线上对应点的正向切线的转角是一个与曲线的选择无关的常数，称其为映射在定点的转动角度。②过一定点的象曲线上一动点到定点的距离与原象曲线上对应点的距离之比，当动点沿曲线趋向定点时的极限为一与曲线的选取无关的常数，称其为映射在定点的伸缩率。上述性质①有一种等价的形式：①′过定点的任意两条曲线经映射后其转角的大小及方向均不变，形象地称这一性质为同向保角性，①′与②一起表明在一定点附近的一个小三角形，与其象“三角形”（一般是曲边三角形）近似地同向相似，称其为保形映射。

　　保形映射的基本定理是黎曼映射存在唯一性定理，它断言：若D是一个边界点集多于一个点的单连通区域，Z0∈D，则一定存在唯一确定的解析函数w＝f（Z）将D双方单值保形映射为单位圆｜w｜＜1，且使f（Z0）＝0，f′(Z0)＞0，这一定理在1851年作为B.黎曼的博士论文题目提出后，100多年来已被许多数学家用多种方法证明，并将其推广到多连通区域的情形，在黎曼映射定理提出之后，C.卡拉西奥多里证明了边界对应定理，即在黎曼映射定理的条件下 ，若бD＝ L是一条简单闭曲线，则映射函数f（Z）可以连续开拓到L上且实现L与｜w｜＝1之间的双方单值连续映射。

处处连续处处不可导函数

可导的误区

第一个处处连续处处不可导函数

理论的运用

爱华网本文地址 » http://www.aihuau.com/a/25101016/315884.html