教学目标
1、知识与技能
①理解正比例函数的概念及正比例函数图象特征。
②知道正比例函数图象是直线,会画正比例函数的图象;进一步熟悉作函数图象的主要步骤。
2、过程与方法
①通过“燕鸥飞行路程问题”的探究和学习,体会函数模型的思想。
②经历运用图形描述函数的过程,初步建立数形结合,经历探索正比例函数图象形状的过程,体验“列表、描点、连线”的内涵。
3、情感态度与价值观
①结合描点作图培养学生认真细心严谨的学习态度和习惯。
②培养学生积极参与数学活动,勇于探究数学现象和规律,形成良好的质疑和独立思考的习惯。
教学重点:探索正比例函数图形的形状,会画正比例函数图象。
教学难点:正比例函数解析式的理解
教学方法:探索归纳,启发式讲练结合
教学准备:多媒体课件
教学过程设计
一.提出问题,创设情境
情境1、
(1)你知道候鸟吗?
(2)它们在每年的迁徙中能飞行多远?
(3)燕鸥的飞行路程与时间之间有什么样的数量关系?
教师用课件展示问题。让学生观察图片中的燕鸥,然后思考并解答课本上的问题。学生自主解决--三个问题。教师在学生得到结论的基础上提醒:这里用函数y=200x对燕鸥飞行路程和时间规律进行了刻画。
【设计意图】从具体情境入手,让学生从简单的实例中不断抽象出建立数学模型、数学关系的方法。
二.导入新课,引出概念
P123 思考 1、写出下列问题中的函数表达式
(1)圆的周长l随半径r的大小变化而变化
(2)汽车在公路上以每小时100千米的速度行驶,怎样表示它走过的路程S(千米)随行驶时间t(小时)变化的关系?
(3)每个练习本的厚度为0.5cm,一些练习本摞在一起的总厚度长(单位:cm)随这些练习本的本数n的变化而变化
(4)冷冻一个0度的物体,使它每分下降2度,物体的温度T(单位:度)随冷冻时间t(单位:分)的变化而变化
2、这些函数有什么共同点?这样的函数我们把它们称为正比例函数。
(4)由上得到的启发,你能试着给正比例函数下个定义吗?
学生先自主探究,后分组讨论,然后教师让各小组代表回答问题。师生互动对回答的问题进行分析评价。
【设计意图】通过这些实际问题使学生进一步加深对函数概念的理解,也为导出正比例函数概念做好铺垫。
教师引导学生观察分析上面的四个表达式的共性:都是常数与自变量乘积的形式。教师口述并用幻灯片展示正比例函数的概念。
一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.
教师让学生看书,在定义处画上记号,并提出问题:这里为什么强调k 是常数,k≠0?
上述问题中各正比例函数的比例系数分别是什么?(由学生一一说出)
做一做:下面的函数是不是正比例函数?
y=3xy=2/xy=x/2s=πr2
通过上面的例子,师生共同总结正比例函数须满足下面两个条件:
1、比例系数不能为0
2、自变量X的次数是一次的。
【设计意图】通过归纳、分析使学生明白正比例函数的特征、理解其解析式的特点。
我们现在已经知道了正比例函数关系式的特点,那么它的图象有什么特征呢?
四、认识扩大
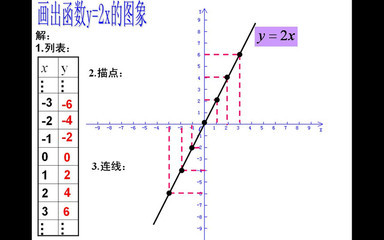
[活动]各小组合作回顾函数图象的画法,画出下列函数的图象(1)y=2x(2)y=-2x(P111 例1)
活动设计意图:通过活动,了解正比例函数图象特点及函数变化规律,让学生自己动手、动口、动脑,经历规律发现的整个过程,从而提高各方面能力及学习兴趣.
教师活动:引导学生正确画图、积极探索、总结规律、准确表述.
学生活动:利用描点法正确地画出两个函数图象,在教师的引导下完成函数变化规律的探究过程,并能准确地表达出,从而加深对规律的理解与认识.
活动过程与结论:
1.函数y=2x中自变量x可以是任意实数.列表表示几组对应值:
x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
y | -6 | -4 | -2 | 0 | 2 | 4 | 6 |
画出图象如图P124
2.y=-2x的自变量取值范围可以是全体实数,列表表示几组对应值:
x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
y | 6 | 4 | 2 | 0 | -2 | -4 | -6 |
画出图象如图P124.
问:①、观察两个函数图象,能得到那些信息?
教师指导:观察函数图象从以下几个方面进行(1)自变量(2)函数值(3)升降性(4)特殊点(5)过了那几个象限(6)图象的形状
②、总结正比例函数图象的性质
3.两个图象的共同点:都是经过原点的直线.
不同点:函数y=2x的图象从左向右呈上升状态,即随着x的增大y也增大;经过第一、三象限.函数y=-2x的图象从左向右呈下降状态,即随x增大y反而减小;经过第二、四象限.
尝试练习:1、判断下列函数那些是正比例函数
(1)y=2x(2)y=kx(k≠0) (3)y=-1/3x(4)y=1/2x+2(5)y=3x2 (6)y=-3x2
2、P124 练习
比较两个函数图象可以看出:两个图象都是经过原点的直线.函数的图象从左向右上升,经过三、一象限,即随x增大y也增大;函数 的图象从左向右下降,经过二、四象限,即随x增大y反而减小.
总结归纳正比例函数解析式与图象特征之间的规律:
正比例函数y=kx(k是常数,k≠0)的图象是一条经过原点的直线,我们可称它为直线y=kx.当k>0时,直线y=kx经过一、三象限,从左向右上升,即y随x的增大而增大;当k<0时,直线y=kx经过二、四象限,从左向右下降,即y随x的增大而减小。
五、认识的深化
[活动二]
活动内容设计:
1、经过原点与(1,3)的直线是哪个函数的图象?若经过原点与(1,-4)呢?你发现了什么?
2、画下比例函数时,怎样画最简便?为什么?
活动设计意图:通过这一活动,让学生利用总结的正比例函数图象特征与解析式的关系,完成由图象到关系式的转化,进一步理解数形结合思想的意义,并掌握正比例函数图象的简单画法及原理.
教师活动:引导学生从正比例函数图象特征及关系式的联系入手,寻求转化的方法.从几何意义上理解分析正比例函数图象的简单画法.
学生活动:在教师引导启发下完成由图象特征到解析式的转化,进一步理解数形结合思想,找出正比例函数图象的简单画法,并知道原由.
活动过程及结论:经过原点与点(1,k)的直线是函数y=kx的图象.画正比例函数图象时,只需在原点外再确定一个点,即找出一组满足函数关系式的对应数值即可,如(1,k).因为两点可以确定一条直线.
随堂练习:1、说出下列函数性质(1)y=5x(2)y=-5x
2、P125 练习
六、总结归纳,布置作业
问题:在本节课中,我们经历了怎样的过程,有怎样的收获?
本节课我们通过实例了解了正比例函数解析式的形式及图象的特征,并掌握图象特征与关系式的联系规律。在以后的学习中,我们将继续这样的思路来研究各种具体的函数,根据它们的共同结构给它们取名,画出函数的图象并研究它们的性质。
作业:
1、P120习题14.2─1、2题.
2、某函数具有下面的性质:它的图象是经过原点的一条直线.且y随x增大反而减小.请你举出一个满足上述条件的函数,写出解析式,画出图象.
备选题:
1、若函数y=(6+3m)x+4n-4是正比例函数,求m、n
2、当k=______时,y=(k+3)x2k-1是正比例函数
 爱华网
爱华网



