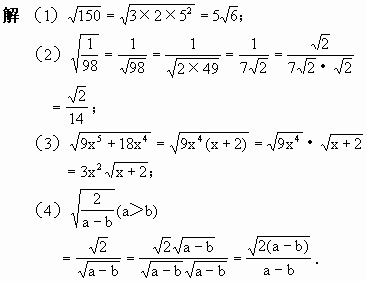昨天开始了《理解复变函数》的写作,本意确实是想交流一下思考结果,但是没有想到!!!!!咱们电气学院的谭院也转了…….顿时…….因为里面有不和谐的词汇。好在谭院说可以忽略,我想就按照之前的语气讲下去,不要让这种文章变得太枯燥。
谭院看了文章希望我能再讲一些东西,一个是卷积,一个是i对于二维维度的含义。卷积绝对是个老大难,我也看了很多关于卷积的文章才能建立起一种直观的印象。卷积的理解也有很多种,卷积理解好了,对后面的傅立叶变换、拉普拉斯变换的理解有很大帮助。卷积先不讲,必须要放到复变函数后面。本意这一部分是要讲复变函数的,但是谭院的建议让我觉得,i有必要再结合二维维度讲一下。所以这一部分还要讲i ,而实际讲的时候会穿插在一起。
之前的部分所有的公式都是用Word的字符打出来的,看起来不是太方便,所以这一篇还有后面的关于公式或者字母一律用Mathtype编辑。
再讲之前还要扯一点直觉这个东西。数学的公理化定义确实为数学的发展作出的巨大贡献,但是对于普通人理解数学产生了比较大的障碍。刚进大学就学高数,高数中关于极限的定义是经典的语句。我看到这里,又不禁要问,这他妈是啥!
简单举个栗子,关于函数在某一点的极限:
设函数在点某一去心邻域有定义,如果存在常数A,对于任意给定的正数(不论他多么小),总存在正数,使得当x满足不等式时,对应的函数值都满足不等式,那么常数A就叫做函数当的极限。

坑爹呢这是!
定义到这里就结束了,看似很难懂,其实三句话就可以解释清楚。当无限趋近于时,就无限趋近于A,那么A就叫做在趋近于的极限。第一句话,对应着这个不等式。第二句话对应着这个不等式。这就是直觉性理解和公理化定义的区别。就好比一首美妙的曲子,写在谱上,虽然可以流传很久保存很久,但是没有人把它“翻译”过来变成一首曲子,没有人会体会到它的美妙。
————————————————————————割————————————————————————
这里补充一下上一篇的遗漏。上一篇少说了一个复数的幂和开根运算。
根据著名的棣莫弗定理:
复数的n次幂的模等于这个复数的模的n次幂,它的辐角等于这个复数的辐角的n倍。
其实利用了极坐标的形式即之后,幂运算和开根运算就都很好理解了。首先复数是有周期性的,一个[]复数旋转了之后还是它自己,所以。那么就是幅值开n次根,辐角变为原来的。
在某种程度上来说,线性代数式这种形式仍然是用实数的思想处理复数。而这种极坐标形式才是处理复数的新思维。但是在具体问题上,两种方法各有优点。
下面继续讲i。
i的出现确实是为了解决一些高次方程而引入的,在引入初期,它是纯代数的。在历史上的几次数集扩充当中,每次“新造”的数都要满足之前的一些运算法则,还要满足一些数的基本规律,比如说大小。就像现在的软件向下兼容一样。
但是i的出现改变了这个规律,它的运算是基于对以往的实数运算的修正上的。大家可以思考一下和中的根号“”是一样的含义吗?
事实上在实数域内,仅仅是一个数,或者一个点。到了复数域,它就是两个点了。套用上面的公式,它分别表示了和这两个点。
复数是没有大小的,因为到了平面上,点就没有了“序”的概念了,就好比向量没有办法比较大小。
复变函数到后来的发展与矩阵结合起来,复数可以用一个矩阵来表示。
举一个最简单的栗子,还是i。i表示旋转90度,而到了线性空间中,矩阵也表示把一个点旋转90度。再反过来举个栗子,矩阵的的转置对应着复数的共轭,这个有兴趣的朋友可以往下研究。
这就是数学的魅力,两个不同的体系,竟能有如此高的相似,一个复数可以是指一个点,也可以表示一个变换。同样,一个点可以用一个向量矩阵来表示,左乘一个矩阵也完成了一个变换。
在笛卡尔坐标系中,我们可以用有序实数对来表示一个点。而到了复数域,一个点只需要一个数来表示,因为本身就是一个数。虽然这个数是一个复数,而这个复数又是用两个实数和虚数单位i的线性组合构成的。
对函数的学习,需要函数图像的帮助。想到高中各种抛物线、双曲线,都隐隐觉得那段日子真的很美好啊!那么,复变函数有没有图像呢?有!不过事实上你看不到(随着四维图学的兴起,给描述四维图形提供了手段,复函数图形的表示也不再困难)。因为复变函数的z实际上是一个二元函数,,这里的x和y是自变量,复平面上的某一点(x,y)映射到w上的某一点(u,v)之间的关系,一般都有2个二元实数函数相联系,也就是说因变量也是二维的,因此复变函数的图形是四维的。四维的图形自然无法在三维的直角坐标系里画出来。这恰恰是拓扑学的重要课题。比如说,一个代数函数,在二维复数空间里面代表的就是一张黎曼曲面。这是二维复数空间的子流形。当然一般不研究这个流形的微分结构(解析结构),那是复分析已经基本上完成的事情。一般研究的是这个流形的拓扑或者同伦性质,最直接的就是同伦相关的问题。实际上代数函数的图像一般都是多连通的,所以一般来说同胚于多环面(实际上这研究的是欧拉数的问题)。再深入的有黎曼-罗赫定理。研究复变函数的这种几何性质是代数几何的重要课题。引用一段话:
复变函数理论的出发点,是复平面的拓扑学性质。在复平面上用开圆盘作拓扑基可以得到其普通拓扑。而通过球极投影(将复平面上的点同一个球上的点对应起来),可以引入扩充复平面,这个扩充平面比复平面多了一个无穷远点(不是一个复数,而是一个额外的点),从而变成了紧集。在开平面(复平面)或者闭平面(添加了无穷远点的复平面)上都可以定义其到自身的映射,这种映射就是复变函数。
(注:这里说的球极投影,可以理解为在复平面上,放置一个球体,与的切点为原点,这个切点叫做“南极”,用直线连接“北极”和复平面每一个点,与球面的交点就是复平面上的点在球面上的投影)
再详细一点,从几何的角度上看,复变函数是一个复平面上的点集到另一个复平面上的一个映射。在直角坐标系复平面上,自变量记作,函数值记作。那么复变函数就等价于两个二元函数,,即一个复变函数的映射,等同于两个二元实函数的映射。其中如果u和v满足一些特定的条件,这个复变函数w就变得非常特殊,这个后面再讲。
其实到了高等数学的多元函数阶段,就会有一个场field的概念。这个field可以用一个function表示。而我们碰到的很多函数都是标量场scalar field,确定了自变量x,y的值,确定了这个位置上的函数值。而描述矢量场vector field的function不仅确定了位置大小,还确定了方向。基本形式是这样,
其中,A表示一个矢量场函数,函数P、Q、R分别确定了在某个点上的x、y、z轴上分量的大小,而i,j,k则表示三个正交方向的单位向量。只要给定了位置即x,y,z的值,那么在这个点上就有一个矢量,这个矢量并不能实际画出来,但是在这个场下这个点具有一个性质,这就是矢量场。
利用这样的思想,就可以分析复变函数了。
我们先画出一个的直角坐标系,同理,给定一组x,y的值,也就确定了一个复数,而这个复数没有办法画出来,因为并不实际存在于平面,但是这个位置的点确实有这样的性质,这样子复变函数就建立起来了。
之前说到的“一些特定的条件”,就“柯西-黎曼”方程。复变函数的可微性的要求比实变函数要高得多,由此将引出解析函数的概念。
解析函数就是实函数和都连续可微,同时满足柯西-黎曼方程的复变函数。
对于柯西-黎曼方程的理解,我还没有理解透。我只理解了前面一个方程。下面谈一下我的理解。
解析函数既然可微,解析函数对x,y求偏导之后也必定是解析函数,换句话说,既然连续,自然要可积。利用高等数学的知识,一个解析函数可以写成全微分方程的解。而这个式子是全微分方程的充要条件就是。这就是对柯西-黎曼方程的第一个方程的理解。神马?为什么满足了方程就是全微分?一句话就可以解释,连续函数的偏二阶导的结果与求导顺序无关。(PS.这一段我花了很久才想明白….希望能有朋友解释一下后面一个方程,千万不要是公式的证明,而是可以用语言叙述的东西,这样才能体现出直觉性,更能让人理解)
这一篇写的很难受,因为把公式录入到人人日志中很困难,太坑爹了。下一部分写复变函数的积分和复级数。
 爱华网
爱华网