让我们先了解一下一位加法器。假定您现在需要将一位数加在一起并算出答案,为此开始设计电路时所采用的方式是首先查看所有逻辑组合。您可以查看以下四组数的求和:
| 0 | 0 | 1 | 1 |
| +0 | +1 | +0 | +1 |
| 0 | 1 | 1 | 10 |
在您遇到1+1之前,一切情况都很正常。在1+1的情况下,您需要考虑比较麻烦的进位问题。如果不考虑进位(因为这毕竟是1位加法问题),您会发现可通过异或门电路来解决此问题。但是如果考虑进位,则可能要改写等式,从而始终包括2位输出,如下所示:
| 0 | 0 | 1 | 1 |
| +0 | +1 | +0 | +1 |
| 00 | 01 | 01 | 10 |
通过这些等式,您可以生成下面的逻辑表:
| ||||||||||||||||||||
通过查看该表,您会发现可通过异或门电路来实现Q,通过与门电路来实现CO(进位输出)。一切都很简单。
如果要将两个8位的字节加在一起,又要如何处理呢?实现该操作要稍微难一些。最简单的方法是将该问题模块化为可重用的元件,然后复制这些元件。这种情况下,我们只需要创建一个元件:全二进制加法器。
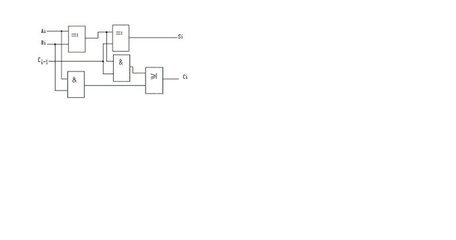
我们发现全加法器和上述加法器之间的差别在于全加法器可将A、B输入与进位输入(CI)输入相加。拥有全加法器之后,我们可以将8个这样的全加法器串接在一起,从而形成一个字节宽的加法器,并将进位输入从一个加法器级联到另一个加法器。
与我们前面使用的逻辑表相比,全加法器的逻辑表稍微复杂一些,原因是我们现在有3个输入位。该逻辑表如下所示:
| |||||||||||||||||||||||||||||||||||||||||||||
有多种不同的方法来实现该表,在此我们将介绍一种易于理解的方法。如果您查看Q位,会发现顶部4位的工作方式与针对A和B的异或门电路类似,而底部4位的工作方式与针对A和B的同或门电路类似。同样,CO顶部4位的工作方式与针对A和B的与门电路类似,而底部4位的工作方式则和或门电路类似。根据这些事实,下面的电路可实现全加法器:
这当然不是实现全加法器最有效的方法,但却极易理解,并且很容易跟踪使用该方法的逻辑。如果有兴趣,您可以思考一下如何使用更少的门电路来实现该逻辑。
现在我们有了一个名为“全加法器”的功能。计算机工程师下一步要做的是将全加法器装在“黑盒子”中,这样他就不用考虑该元件的细节了。用于全加法器的黑盒子将如下所示:
通过这个黑盒子,现在很容易就可画出一个4位全加法器:
在该电路图中,每一位的进位输出将直接输入到下一位的进位输入。通过硬连线方式将最初的进位输入位设为0。如果在A和B线路上输入两个4位的数字,则将会在Q线路上获得该4位数的和输出,另外还有1位用来表示最终进位输出。你会发现该链可随意扩展,如果需要,可扩展到8位、16位或32位。
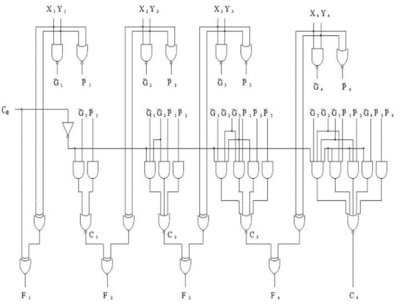
我们刚刚创建的4位加法器称为行波进位加法器。之所以称为行波进位加法器,是因为进位位像波纹一样从一个加法器输入到另一加法器。该实现方式的优点在于它非常简单,但其缺点是存在速度问题。在实际电路中,门电路的状态切换需要时间(该转换时间属于纳秒级,但对于高速计算机来说纳秒也是很重要的)。由于存在行波进位,因此32或64位的行波进位加法器可能需要100到200纳秒来获得最终的求和结果。为此,工程师创建了更高级的名为先行进位加法器的加法器。实现先行进位加法器所需的门电路数量很大,但是该加法器在计算速度上大有改进。
 爱华网
爱华网