梯形数值积分,通过已知参数x,y按dim维使用梯形公式进行积分
例1 计算int(sin(x),0,pi)
- %by dynamic
- %all rights reserved by www.matlabsky.com
- >>x=0:pi/100:2*pi;
- >>y=sin(x);
- >>z=trapz(x,y)%或者说使用z =pi/100*trapz(y)
- z =
- 1.0300e-017
- >>z = pi/100*trapz(y)
自适应simpson公式数值积分,适用于精度要求低,被积函数平滑性较差的数值积分
注意事项:
1.被积函数fun必须是函数句柄
2.积分限[a,b]必须是有限的,因此不能为inf
3.p1为其他需要传递的参数,一般是数值
可能警告:
1.'Minimum step size reached'
意味着子区间的长度与计算机舍入误差相当,无法继续计算了。原因可能是有不可积的奇点
2.'Maximum function count exceeded'
意味着积分递归计算超过了10000次。原因可能是有不可积的奇点
3.'Infinite or Not-a-Number function value encountered'
意味着在积分计算时,区间内出现了浮点数溢出或者被零除。
例2 计算积分1/(x^3-2*x-p),其中参数p=5,积分区间为[0,2]
- %by dynamic
- %all rights reserved by www.matlabsky.com
- >>F = @(x,n)1./(x.^3-2*x-n);
- >>Q = quad(@(x)F(x,5),0,2)%或者使用quad(F,0,2,[],[],5)效果是一样的,只是前者使用的函数嵌套
- Q =
- -0.4605
- >>quad(F,0,2,[],[],5)
- ans =
- -0.4605
自适应Lobatto数值积分,适用于精度要求高,被积函数曲线比较平滑的数值积分
注意事项:
同quad
可能警告:
同quad
例3 计算积分1/(x^3-2*x-p),其中参数p=5,积分区间为[0,2]
- %by dynamic
- %all rights reserved by www.matlabsky.com
- >>F=@(x,p)1./(x.^3-2*x-p);
- >>Q = quadl(F,0,2,[],[],5)%或者Q =quadl(@(x)F(x,5),0,2)
- Q =
- -0.4605
自适应Gauss-Kronrod数值积分,适用于高精度和震荡数值积分,支持无穷区间,并且能够处理端点包含奇点的情况,同时还支持沿着不连续函数积分,复数域线性路径的围道积分法
注意事项:
1.积分限[a,b]可以是[-inf,inf],但必须快速衰减
2.被积函数在端点可以有奇点,如果区间内部有奇点,将以奇点区间划分成多个,也就是说奇点只能出现在端点上
3.被积函数可以剧烈震荡
4.可以计算不连续积分,此时需要用到'Waypoints'参数,'Waypoints'中的点必须严格单调
5.可以计算围道积分,此时需要用到'Waypoints'参数,并且为复数,各点之间使用直线连接
6.param,val为函数的其它控制参数,比如上面的'waypoints'就是,具体看帮助
出现错误:
1.'Reached the limit on the maximum number of intervals inuse'
2.'Infinite or Not-a-Number function value encountered'
计算有奇点积分int(exp(x)*log(x),0,1)
%by dynamic
%all rights reserved by www.matlabsky.com
>>F=@(x)exp(x).*log(x);%奇点必须在端点上,否则请先进行区间划分
>>Q =quadgk(F,0,1)
Q =
-1.3179
五、[Q,fcnt] =quadv(fun,a,b,tol,trace)
矢量化自适应simpson数值积分
注意事项:
1.该函将quad函数矢量化了,就是一次可以计算多个积分
2.所有的要求完全与quad相同
计算下面积分,分别计算n=1,2...,5时的5个积分值,被积函数1/(n+x),积分限为[0,1]
%by dynamic
%all rights reserved by www.matlabsky.com
>>for k =1:5,Qs(k) = quadv(@(x)1/(k+x),0,1);end;Qs
Qs =
0.69310.40550.28770.22310.1823
>>F=@(x,n)1./((1:n)+x);%定义被积函数
>>quadv(@(x)F(x,5),0,1)%我们可以完全使用quadv函数替换上面循环语句的,建议使用后者
ans =
0.69310.40550.28770.22310.1823
六、q =dblquad(fun,xmin,xmax,ymin,ymax,tol,method)
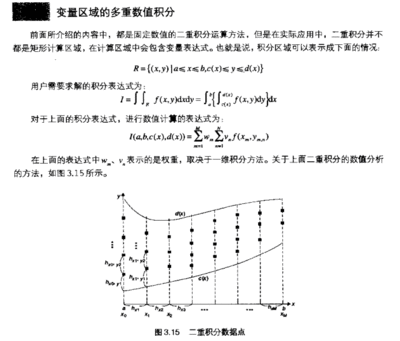
矩形区域二重数值积分,一般区域二重积分参见NIT(数值积分工具箱)的quad2dggen函数
七、q=triplequad(fun,xmin,xmax,ymin,ymax,zmin,zmax,tol,method)
长方体区域三重数值积分,注意此时没有一般区域的三重积分
下面总结下:
(1)quad:采用自适应变步长simpson方法,速度和精度都是最差的,建议不要使用
(2)quad8:使用8阶Newton-Cotes算法,精度和速度均优于quad,但在目前版本下已被取消
(3)quadl:采用lobbato算法,精度和速度均较好,建议全部使用该函数
(4)quadg:NIT(数值积分)工具箱函数,效率最高,但该工具箱需要另外下载
(5)quadv:quad的矢量化函数,可以同时计算多个积分
(6)quadgk:很有用的函数,功能在Matlab中最强大
(7)quad2dggen:一般区域二重积分,效率很好,需要NIT支持
(8)dblquad:长方形区域二重积分
(9)triplequadL:长方体区域三重积分
1 被积函数带参数的积分
题目:
函数为 y=sin(k*x)*x^2,对x积分,
积分区域为【1,5】,目的是要画 k 和 y 的图形.
方法一
%带参数积分
clear all
k=linspace(1,5);
for i=1:length(k)
kk=k(i);
fun=inline(subs('sin(k*x)*x^2','k',kk));
y(i)=quadl(fun,1,5);
end
hold on;
plot(k,y,'r')
方法二 利用匿名函数+循环
f=@(k) quad(@(x)sin(k.*x).*x.^2,0,5)
kk=linspace(0,5);
y=zeros(size(kk));
for ii=1:length(kk)
y(ii)=f(kk(ii));
end
plot(kk,y)
方法三 匿名函数+arrayfun函数
plot(linspace(0,5),arrayfun(@(k) quad(@(x)sin(k.*x).*x.^2,0,5),linspace(0,5)))
隆重推介Matlab工具箱的Mupad解,超简洁,我近来暑假刚好研究这个,所以写一下这个的解法,前面博文有这个的教程~~
稍微一改就是一道二重积分问题
题目:
函数为 H=sin(k*x)*y^2,对x积分再对y积分,
积分区域都是【1,5 】,目的是要画 k 和 H 的图形
 爱华网
爱华网