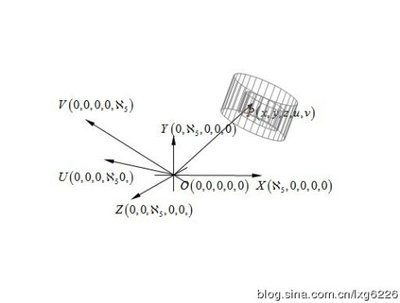
在现有中外的大学和研究院所的几何学教材中,各国的数学家,科学家,信息学家和教师都习惯用“无穷多∞”或者“无穷大∞”来描述几何学上的各种并不相等的“无穷大”。这其实是一种非常不好的错误习惯。康托在“集合论”中,认真地、仔细地区分开了几何学中常见的各个不相等的“无穷大”。他把“最小的无穷大”,即“可数的离散无穷大”称作为“阿列夫零”,把不可数的连续无穷作了精细的类别划分,将“不可数的连续弯曲点的总数所构成的无穷大”称作为“阿列夫一”,将“不可数的连续曲线的总数所构成的无穷大”称作为“阿列夫二”,将“不可数的连续曲面的总数所构成的无穷大”称作为“阿列夫三”,将“不可数的连续弯曲体的总数所构成的无穷大”称作为“阿列夫四”,……,等等。【相关的重要链接:漫谈数学变量语言文字系统(3)】
换言之,在康托连续集合学中,其一维曲线空间中,主要是描述各种连续点,处处连续存在n阶导数的点和处处连续存在阿列夫零阶导数的点,以及不连续的各种奇点和处处不连续的各种奇点等等。上述各种点的总数是阿列夫一。因此,可以描述连续弯曲点的这种一维曲线座标系的座标轴上的连续点的总数是阿列夫一。
在二维曲线座标系中,由于各种连续曲线和不连续曲线的总和是阿列夫二,因此,可以描述连续曲线的二维曲线座标系连续点的总数是阿列夫二,要比一维曲线座标系的座标轴上的上的连续点的总数更加稠密。
在三维曲线座标系中,由于各种连续曲面和不连续曲面的总和是阿列夫三,因此,可以描述连续弯曲体表面的三维曲线座标系的座标轴上的连续点的总数是阿列夫三。
在四维曲线座标系中,由于各种连续弯曲空间(连续弯曲体)和不连续弯曲空间(不连续弯曲体)的总和是阿列夫四,因此,可以描述连续弯曲体内外的四维曲线座标系的座标轴上的连续点的总数是阿列夫四。
在五维曲线座标系中,由于各种连续弯曲超体和不连续弯曲超体的总和是阿列夫五,因此,可以描述连续弯曲超体内外的四维曲线座标系的座标轴上的连续点的总数是阿列夫五。
……,诸如此类,用不着继续赘述了。
不仅如此,我们还必须要彻底纠正在现有中外的大学和研究院所的几何学教材中,各国的数学家,科学家,信息学家和教师都习惯用“无穷少ε”或者“无穷小ε”来描述几何学上的各种并不相等的“无穷小”的错误习惯。
在“康托无穷超实数集合学”中,不仅将原先那种不可数的“连续实数集合”扩增无穷多个的“阿列夫无穷多数”或者“阿列夫无穷大数”,还必须要扩增无穷多个的“倒易阿列夫无穷多数”或者“倒易阿列夫无穷大数”,即扩增无穷多个“无限少数”或者“无限小数”。之后,才能满足“连续度量几何学”的实际必需。直言之,任何一种“连续度量几何学”,只有在这种“康托超无限实数集”中,才能被完整、全面、系统、而且精确、准确、正确地加以描述。仅有以往的那种“实数集”,远远无法满足“连续度量几何学”的实际需要的。
一维曲线上的任何一个连续点处的无限小邻域为倒易阿列夫1,
二维曲面上的任何一个连续点处的无限小邻域为倒易阿列夫2,
三维曲面上的任何一个连续点处的无限小邻域为倒易阿列夫3,
四维弯曲体中的任何一个连续点处的无限小邻域为倒易阿列夫4,
五维弯曲超体中的任何一个连续点处的无限小邻域为倒易阿列夫5,
……,等无穷多种无限小倒易阿列夫邻域,一律都是两两不相等的无限小邻域。
在康托连续度量几何学中,几何空间的维数越高,超无限的连续点数就愈加稠密。反之,几何空间的维数越低,超无限的连续点数就愈加稀疏。
相关的重要链接:
非线性科学和线性科学举例——非惯性物理学和惯性物理学(信息文明启蒙主义
漫谈数学变量语言文字系统(3)
不同几何空间维数的座标系之间极为深刻的本质差别
 爱华网
爱华网