单摆周期公式的数学推导
一、单摆周期公式:
单摆周期仅摆长L相关,与L的平方根成正比。公式如下:
g是重力加速度,一般取9.8m/ss。
二、采用牛顿第二定律推导:
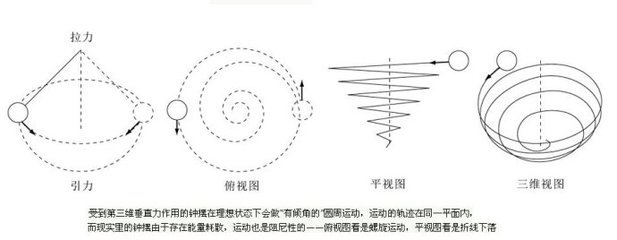
如下图,摆长为l,重物受力为:重力mg和绳子的张力T。取如图所示的二维坐标系,张力T可以分解为垂直和水平方向的二个力。L与垂线的夹角为θ。
根据牛顿第二运动定律,F=ma,可以列出重物在x和y二个方向上的运动方程:
这二个微分方程相当难解,所以只能采用一种“小角度近似”的方法进行处理,
解的物理意义很明确,A是最大振幅,ω是角速度,φ是初相角(视初始条件而定)。
三、采用机械能守恒定律推导:
重物的机械能,可以分为动能和势能:ME=KE+u(ME为总机械能,KE为动能,u为势能)。在重物摆动过程中,其机械能保持不变,为一恒定常数。而动能KE=1/2mvv(m为重物质量,v为速度,这里用二个v表示平方);势能u=mgy(设下图中x坐标线为0势能,则任意点P处重物高度为y)。

推导过程和解微分方程是微积分学的知识,高中知识是无法推导的。
从上述二个推导过程看,均采用了小角度近似方法,似乎对结论有一定影响。但最终的结果中,周期与角度θ是无关的,因而该公式即为理论推导结果。
上述推导过程整理自MIT的LW教授所授普通物理视频课程,网易有下载。
 爱华网
爱华网