高考物理第一轮复习同步导学
§4.7 万有引力定律及其应用
【考点自清】
一、开普勒三定律
(1) 开普勒第一定律(轨道定律):所有的行星围绕太阳运动的轨道都是椭圆,太阳处在所有椭圆的一个焦点上.
每个椭圆有两个焦点,所有行星运动的椭圆轨道均有一个焦点是相互重合的,太阳就处在这个重合的一个焦点上;不同行星绕太阳运行时的椭圆轨道是不同的。
(2) 开普勒第二定律(面积定律):对任意一个行星来说,它与太阳的连线在相等的时间内扫过相等的面积.
行星运动的线速度大小在轨道上各点是不同的;行星近日点的速率大于远日点的速率。
(3) 开普勒第三定律(周期定律):所有行星的轨道的半长轴的三次方跟它的公转周期的二次方的比值都相等.
即(M为中心天体质量)K是一个与行星无关的常量,仅与中心天体有关.
在近似情况下,通常将行星或卫星的椭圆轨道运动处理为圆轨道运动.
二、万有引力定律
(1)内容:自然界中任何两个物体都是相互吸引的,引力的大小跟两个物体的质量的乘积成正比,跟他们之间的距离的二次方成反比.
(2)公式:,叫引力常量.
(3)适用条件:严格来说公式只适用于质点间的相互作用,但当两物体的距离远大于物体本身大小时,物体可视为质点,公式也近似适用,但此时r应为两物体质心间距离;均匀的球体可视为质点,r是两球心间的距离.
(4)对万有引力定律的理解:
①普遍性:两个物体之间相互作用的引力是一对作用力和反作用力,符合牛顿第三定律.
②相互性:微观粒子由于质量都非常小,粒子之间的万有引力很不显著,因此可以忽略不计,通常情况下物体间的引力非常小,一般可忽略不计,只有质量巨大的天体之间或天体与一般物体之间的万有引力才有宏观上的意义.
③宏观性:万有引力是普遍存在于宇宙间任何有质量的物体(小到微观粒子大到天体)之间的相互作用力,是自然界物体见的基本相互作用之一.
【重点精析】
一、对开普勒行星运动定律的理解
⑴开普勒定律是总结行星运动的观察结果而总结归纳出来的,它们都是经验定律,都是从观察行星运动所取得的资料中总结出来的,开普勒行星运动定律只涉及运动学、几何学等方面的内容。
⑵圆周运动可看成是椭圆运动的特例.在一般情况下,可把行星运动当作圆周运动来处理,此时,R为圆周运动的半径,T为圆周运动的周期.
⑶常量k仅与太阳的质量有关而与行星无关.这个规律也可推广到宇宙间其它的天体系统(如地球和卫星系统),常量k仅与该系统的中心天体质量有关而与周围绕行的星体无关.中心天体不同的系统k值不同,中心天体相同的系统里k值是相同的.
【例1】某行星绕太阳沿椭圆轨道运行,它的近日点到太阳的距离为r,远日点到太阳的距离为R,若行星经过近日点的速度大小为vA,求该行星经过远日点时速度大小.
【点评】根据上述计算结果可知,行星在近日点的速率较大,在远日点的速率较小,即行星从近日点到远日点的过程是减速过程,从远日点到近日点的过程是加速过程.
【变式练习1】我国在实现卫星绕月之后,又将实现第二期工程目标,即发射了航天器着陆到月球上.航天器抵达月球的表面时,先绕月球做半径为R的圆周运动,假设其运行周期为T。当航天器快运动到A点时地面控制中心将发出指令,使其速率降低到适当数值,从而使航天器沿着以月心为焦点的椭圆轨道运动,椭圆和月球表面在B点相切,如图所示,这样就可实现航天器在月球的表面登陆.如果月球半径为R0,求飞船由A点到B点所需要的时间.
【点评】在同一天体系统中,绕中心天体运动的“卫星”无论在圆轨道上运行,还是在椭圆轨道上运行,都符合开普勒第三定律,而圆轨道与椭圆轨道虽然在A点相切,但椭圆轨道的半长轴并不等于圆轨道的半径,由此可列方程求解.
二、万有引力定律的适用条件
万有引力定律适用于计算质点间的引力.具体有以下两种情况:
①两物体间的距离远远大于物体本身的线度,两物体可视为质点,例如行星绕太阳的旋转;
②两个均匀的球体间,其距离为两球心的距离.
【例2】如图所示,阴影区域是质量为M、半径为R的球体挖去一个小圆球后的剩余部分.所挖去的小圆球的球心O′和大球体球心间的距离是R/2.求球体剩余部分对球体外离球心O距离为2R、质量为m的质点P的引力.
【点评】万有引力定律只适用于两个质点间的作用,只有对均匀球体,才可将其看作是质量全部集中在球心的一个质点。
【变式练习2】(2009•浙江理综)在讨论地球潮汐的成因时,地球绕太阳的运行轨道与月球绕地球的运行轨道可视为圆轨道.已知太阳质量约为月球质量的2.7×107倍,地球绕太阳运行的轨道半径约为月球绕地球运行的轨道半径的400倍.关于太阳和月球对地球上相同质量海水的引力,以下说法正确的是( )
A.太阳引力远大于月球引力
B.太阳引力与月球引力相差不大
C.月球对不同区域海水的吸引力大小相等
D.月球对不同区域海水的吸引力大小有差异
【解析】由万有引力定律可知,太阳对地球上相同质量水的引力大约是月球引力的170倍,故A正确,B错误;不同海域的水与月球的距离不一样,故引力也不一样,所以C错误,D正确.
【答案】AD
三、万有引力与重力的关系
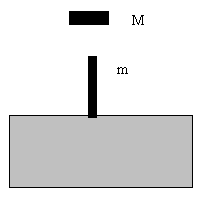
1、重力:重力是指地球上的物体由于地球的吸引而使物体受到的力.通过分析地球上物体受到地球引力产生的效果,可以知道重力是引力的一个分力.引力的另一个分力是地球上的物体随同地球自转的向心力(这个向心力也可以看做是物体受到的地球引力与地面支持力的合力)如图所示.但由于向心力很小,所以在一般计算中可认为重力近似等于万有引力,重力方向竖直向下(即指向地心).
(1)在地面上,忽略地球自转时,认为物体的向心力为零.各处位置均有.
(2)由于Fn=mRω2非常小,所以对一般问题的研究认为Fn=0,.
2、天体表面重力加速度问题
(1)设天体表面重力加速度为g,天体半径为R,因为物体在天体表面受到的重力近似等于受到的万有引力,所以有,(R为星球半径,M为星球质量) .
(2)同样可以推得在天体表面上方高度h处重力加速度.
重力加速度受纬度、高度、地球质量分布情况等多种因素影响,随纬度的增大而增大,随高度的增大而减小.
【例3】 (2009•江苏)英国《新科学家(NewScientist)》杂志评选出了2008年度世界8项科学之最,在XTEJ1650—500双星系统中发现的最小黑洞位列其中,若某黑洞的半径R约为45km,质量M和半径R的关系满足(其中c为光速,G为引力常量),则该黑洞表面重力加速度的数量级为( )
【变式练习3】(2009•全国Ⅱ)如图所示,P、Q为某地区水平地面上的两点,在P点正下方一球形区域内储藏有石油.假定区域周围岩石均匀分布,密度为ρ;石油密度远小于ρ,可将上述球形区域视为空腔.如果没有这一空腔,则该地区重力加速度(正常值)沿竖直方向:当存在空腔时,该地区重力加速度的大小和方向会与正常情况下有微小偏离.重力加速度在原竖直方向(即PO方向)上的投影相对于正常值的偏离叫做“重力加速度反常”.为了探寻石油区域的位置和石油储量,常利用P点附近重力加速度反常现象.已知引力常数为G.
(1)设球形空腔体积为V,球心深度为d(远小于地球半径),PQ=x,求空腔所引起的Q点处的重力加速度反常;
(2)若在水平地面上半径为L的范围内发现:重力加速度反常值在δ与kδ(k>1)之间变化,且重力加速度反常的最大值出现在半径为L的范围的中心.如果这种反常是由于地下存在某一球形空腔造成的,试求此球形空腔球心的深度和空腔的体积.
【思维提升】此题是万有引力定律实际应用的典型实例,求解的关键是综合题中所给信息,充分理解题意,采用补全法求重力加速度反常量值,并结合几何关系等求解空腔深度和体积.
四、应用万有引力定律分析天体的运动
1、基本方法:把天体(或人造卫星)的运动看成匀速圆周运动,其所需的向心力由万有引力提供.
2、解决天体圆周运动问题的两条思路
(1)在地面附近万有引力近似等于物体的重力,F引=mg
(2)天体运动都可以近似地看成匀速圆周运动,其向心力由万有引力提供,即F引=F向.
一般有以下几种表达形式:
3、天体质量和密度的计算
(1)测g法:从中心天体本身出发,利用天体表面的重力加速度g和天体半径R.
(2)环绕法:从环绕天体出发,通过观察卫星绕天体做匀速圆周运动的周期T和轨道半径r进行计算.
③若天体的卫星在天体表面附近环绕天体运动,可认为其轨道半径r等于天体半径R,则天体密度ρ=3π/GT2.可见,只要测出卫星环绕天体表面运动的周期T,就可估算出中心天体的密度.
【例4】已知万有引力常量G,地球半径R,月球和地球之间的距离r,同步卫星距地面的高度h,月球绕地球的运转周期T1,地球的自转周期T2,地球表面的重力加速度g.某同学根据以上条件,提出一种估算地球质量M的方法:同步卫星绕地心做圆周运动,
(1)请判断上面的结果是否正确,并说明理由.如不正确,请给出正确的解法和结果.
(2)请根据已知条件再提出两种估算地球质量的方法并解得结果.
【变式练习4】(2009•全国Ⅰ)天文学家新发现了太阳系外的一颗行星.这颗行星的体积是地球的4.7倍,质量是地球的25倍.已知某一近地卫星绕地球运动的周期约为1.4小时,引力常量G=6.67×10-11N•m2/kg2,由此估算该行星的平均密度约为( D )
五、双星和多星问题
1.双星模型:两星相对位置保持不变,绕其连线上某点做匀速圆周运动.
(1)两星之间的万有引力提供各自所需的向心力.
(2)两星绕某一圆心做匀速圆周运动的绕向相同,角速度、周期相同.
(3)两星的轨道半径之和等于两星之间的距离.
2.“黑洞”是暗物质,它的密度很大,因此产生很大的引力,能将所有物质牢牢地束缚住,就是以光速运动的物质也不能挣脱它的束缚.
【例5】宇宙中存在由质量相等的四颗星组成的四星系统,四星系统离其他恒星较远,通常可忽略其他星体对四星系统的引力作用.已观测到稳定的四星系统存在两种基本的构成形式:一种是四颗星稳定地分布在边长为a的正方形的四个顶点上,均围绕正方形对角线的交点做匀速圆周运动;另一种形式是有三颗星位于边长为a的等边三角形的三个项点上,并沿外接于等边三角形的圆形轨道运行,而第四颗星刚好位于三角形的中心不动.设每个星体的质量均为m.试求二种形式下,星体运动的周期T1和T2.
【名师点金】本题用隔离法求解,即对其中的某星体进行研究,其他星球对该星球的引力的合力提供做圆周运动的向心力.
【规范思维】(1)运动天体的向心力由其他天体的万有引力的合力提供;
(2)运动天体的角速度相等;
(3)天体运动的轨道半径不是天体间的距离,要利用几何知识,寻找两者之间的关系,正确计算万有引力和向心力.
【变式练习5】天文学家将相距较近、仅在彼此的引力作用下运行的两颗恒星称为双星.双星系统在银河系中很普遍.利用双星系统中两颗恒星的运动特征可推算出它们的总质量.已知某双星系统中两颗恒星围绕它们连线上的某一固定点分别做匀速圆周运动,周期均为T,两颗恒星之间的距离为r,试推算这个双星系统的总质量.(引力常量为G)
【同步作业】
1.下列说法正确的是()
A.太阳系中的八大行星有一个共同的轨道焦点
B.行星的运动方向总是沿着轨道的切线方向
C.行星的运动方向总是与它和太阳的连线垂直
D.日心说的说法是正确的
解析:根据开普勒第一定律可知A正确,又因为行星的运动方向总是沿着轨道的切线方向,故B正确,C错误。日心说虽然比地心说又所进步,但是太阳也并非静止,太阳是绕银河系运动的,因而D说法也是错误的。我们一定要注意的是日心说和地心说都有不正确的一面。故本题的正确答案为AB。
2.据《环球时报》报道:“神舟”三号飞船发射升空后,美国方面立即组织力量进行追踪,但英国权威军事刊物《简史防务周刊》评论说,“这使美国感到某种程度的失望”.美国追踪失败的原因是“神舟”三号在发射数小时后,进行了变轨操作,后期轨道较初始轨道明显偏低,如图所示,开始飞船在轨道1上运行几周后,在Q点开启发动机喷射高速气体使飞船减速,随即关闭发动机,飞船接着沿椭圆轨道2运行,到达P点再次开启发动机,使飞船速度变为符合圆轨道3的要求,进入轨道3后绕地球做圆周运动,则飞船在轨道2上从Q点到P点的过程中,运行速率将( )
A.保持不变 B.逐渐增大
C.逐渐减小 D.先减小后增大
解析:由开普勒第二定律可知,飞船与地球的连线在相等的时间内扫过相等的面积,连线越短,单位时间内通过的弧长越长即速率越大.B正确.
4.中子星是恒星演化过程的一种可能结果,它的密度很大.现有一中子星,观测到它的自转周期为T=(1/30)s.问该中子星的最小密度应是多少才能维持该星的稳定,不致因自转而瓦解.(计算时星体可视为均匀球体,引力常量G=6.67×10-11N•m2/kg2)
7.神奇的黑洞是近代引力理论所预言的一种特殊天体,探寻黑洞的方案之一是观测双星系统的运动规律.天文学家观测河外星系大麦哲伦云时,发现了LMCX-3双星系统,它由可见星A和不可见的暗星B构成.两星视为质点,不考虑其他天体的影响,A、B围绕两者连线上的O点做匀速圆周运动,它们之间的距离保持不变,如图所示.引力常量为G,由观测能够得到可见星A的速率v和运行周期T.
(1)可见星A所受暗星B的引力FA可等效为位于O点处质量为m′的星体(视为质点)对它的引力,设A和B的质量分别为m1、m2,试求m′(用m1、m2表示);
(2)求暗星B的质量m2与可见星A的速率v、运行周期T和质量m1之间的关系式.
点击返回《高考物理第一轮复习导学》安排表
 爱华网
爱华网