一、化学动力学基础
二、底物浓度对酶反应速率的影响
三、酶的抑制作用
四、温度对酶反应的影响
五、pH对酶反应的影响
六、激活剂对酶反应的影响
本章重点和习题
一、化学动力学基础
酶促反应动力学(kinetics of enzyme-catalyzedreactions):研究酶促反应的速率以及影响此速率的各种因素的科学。
在探讨各种因素对酶促反应速度的影响时,通常测定其初始速度来代表酶促反应速度,即底物转化量<5%时的反应速度。
(一)反应速率及其测定
反应速率:以单位时间内反应物或生成物浓度的改变来表示。
反应速率的测定:实际上是测定不同时间的反应物或生成物的浓度(物、化方法)。
(二)反应分子数和反应级数
通过反应分子数和反应级数来研究化学反应速率和反应物浓度的关系
1、反应分子数:
在反应中真正相互作用的分子的数目
单分子反应:AP
v=-dc/dt=kc
双分子反应:A+BP+Q
v=-dc/dt=kc1c2
2、反应级数
整个化学反应的速率服从哪种分子反应速率方程式,则这个反应即为几级反应
总反应速率与浓度的关系:
一级反应: 满足单分子反应的速率方程
二级反应:满足双分子反应的速率方程
零级反应:速率与浓度无关
两个不同的概念:
反应分子数:反应机制的问题;
反应级数:反应速率与浓度的关系问题(实际应用中常采用)
(三)各级反应的特征
1、一级反应:反应速率只与反应物的浓度的一次方成正比;半衰期与反应物的初浓度无关;
2、二级反应:反应速率与反应物的浓度的二次方(或两种物质浓度的乘积)成正比;半衰期与反应物的初浓度成反比;
3、零级反应:反应速率与反应物浓度无关而受它种因素影响而改变的反应;半衰期与反应物的初浓度成正比;反应速率为一常数。
二、底物浓度对酶反应速率的影响
(一)中间络/复合物学说
酶催化时,酶活性中心首先与底物结合生成一种酶-底物复合物(ES),此复合物再分解释放出酶,并生成产物。ES的存在已得到实验证实。
(二)酶促反应的动力学方程式
1、米氏方程式的推导:
Michaelis& Menten于1913年推导出一个数学方程式,表示了底物浓度与酶反应速率之间的定量关系,即著名的米氏方程:
1925年,Briggs和Haldane提出稳态理论,对米氏方程做了重要的修正,得到以下方程(也称为米氏方程):
"米氏方程的推导基于以下假设:
1、测定的反应速度为初速度,即反应刚刚开始,产物的生成量极少,逆反应可不予考虑。即式(1)中E+P生成ES的速度极小,可以忽略不计;
2、底物浓度大大超过酶的浓度,[S]》[E],[S]的变化在测定初速度的过程中可忽略不计。
游离酶浓度=总酶浓度-结合到中间产物中酶的浓度
即:[游离酶]=[E]-[ES]
米氏方程的推导
Km的物理意义:当酶反应速率达到最大反应速率一半时的底物浓度,单位是mol/L,与底物浓度的单位一样
根据米氏方程:
(1)当[S]<<Km时,
v=Vmax·[S]/Km=K[S];
(2)当[S]>>Km时,
v=Vmax·[S]/ ·[S]=Vmax;
(3)当[S]=Km时,
v=Vmax·[S]/ ( [S] +[S])=Vmax/2;
2、动力学参数的意义
(1)米氏常数的意义
①Km是酶的一个特性常数:
Km的大小只与酶的性质有关,而与酶的浓度无关;
Km值随测定的底物、反应的温度、pH及离子强度的影响;
不同的酶,Km值不同。如脲酶(25mM)、乳酸脱氢酶(0.017mM)。
② Km 值可以判断酶的专一性和天然底物:
有的酶可作用于几种底物,Km值随底物不同而异,由此可帮助判断酶的专一性;
如蔗糖酶(底物糖蔗:28mM;底物棉子糖:350mM);
1/Km 可近似地表示酶对底物亲和力的大小,1/Km越大,表明亲和力越大;
Km最小的底物称为该酶的最适底物也就是天然底物。
③只有当k3极小时,才能用1/Km来近似地说明酶与底物结合的难易程度;
④可根据已知某个酶的Km值计算出在某一底物浓度时,其反应速率相当于Vmax的百分率;
⑤Km值可以帮助推断某一代谢反应的方向和途径:催化可逆反应的酶,对正逆两向底物的Km值往往是不同的。
(2)Vmax和k3(Kcat)的意义
在一定浓度下,酶对特定底物的Vmax也是一个常数;
k3表示当酶被底物饱和时每秒钟每个酶分子(或是每个活性部位)转换底物的分子数,这个常数又叫转换数(简称TN),通称为催化常数(catalyticconstant,Kcat),单位为s-1;
大多数酶的转换数在1-104s-1之间,Kcat越大,表示酶的催化效率越高。
(3)Kcat/Km的意义
Kcat/Km是E和[S]反应形成产物的表观二级速率常数,有时也称为专一性常数;
Kcat/Km比值的大小,可以比较不同酶或同一种酶催化不同底物的催化效率。比值越大,效率越高。
3、利用作图法测定Km和Vmax值
(1)Lineweaver-Burk双倒数作图法:
优点:方便,应用最广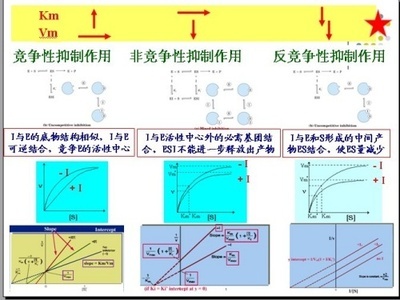
缺点:实验点过分集中于直线的左端,作图不易十分准确。
横轴截距为-1/Km,纵轴截距为1/Vmax,斜率为Km/Vmax
(2)Eadie-Hofstee作图法
纵轴截距为Vmax,斜率为-Km
3. Hanes-Woolf作图法:横轴的截距为-Km,斜率为1/Vmax
4.Eisenthal和Cornish-Bowden直接线性作图法:
方法:把[S]标在横轴的负半轴上,测得的v数值标在纵轴上,相应的[S]和v联成直线,这一簇直线交于一点,其坐标为Km和Vmax;
优点:不需要计算,可直接读出Km和Vmax值;易于识别不正确的观测结果。
(三)多底物的酶促反应动力学
乒乓反应
随机反应
有序反应
三、酶的抑制作用
失活作用(inactivation):使酶蛋白变性而引起酶活力丧失的作用;
抑制作用(inhibition):酶的必需基团化学性质改变,但酶未变性,而引起酶活力的降低或丧失的作用;
抑制剂(inhibitor):能降低酶促反应速度,但不引起酶分子变性失活的物质
(一)抑制程度的表示方法
相对活力分数 a
相对活力百分数 a%
抑制分数 i
抑制百分数 i%
(二)抑制作用的类型及动力学
1、不可逆抑制作用(irreversibleinhibition):抑制剂与酶分子的必需基团共价结合引起酶活性的抑制,且不能采用透析、超滤等物理方法去除抑制剂而使酶复活的抑制作用;
2、可逆抑制作用(reversible inhibition):抑制剂以非共价键与酶分子可逆性结合造成酶活性的抑制,且可采用透析等物理方法去除抑制剂而使酶复活的抑制作用。
可逆抑制作用包括竞争性、反竞争性、和非竞争性抑制几种类型。
竞争性抑制是最常见的一种可逆抑制。增加底物可以消除抑制。抑制剂一般是底物类似物。非竞争笥抑制剂的抑制率不受底物浓度影响。
1、竞争性抑制(competitiveinhibition):
抑制剂与底物竞争与酶的同一活性中心结合,从而干扰了酶与底物的结合,使酶的催化活性降低,称为竞争性抑制作用。
竞争性抑制特点:Km值增大,Vm值不变
2、非竞争性抑制(non-competitive inhibition):
抑制剂既可以与游离酶结合,也可以与ES复合物结合,使酶的催化活性降低,称为非竞争性抑制。
非竞争性抑制的动力学参数:Km值不变,Vm值降低。
3、反竞争性抑制(uncompetitiveinhibition):
抑制剂不能与游离酶结合,但可与ES复合物结合并阻止产物生成,使酶的催化活性降低,称酶的反竞争性抑制。
反竞争性抑制动力学参数:Km减小,Vm降低。
2、可逆抑制剂
可逆抑制剂中最重要,最常见的是:竞争性抑制剂。
竞争性抑制例1:丙二酸类似琥珀酸,抑制琥珀酸脱氢酶;
竞争性抑制例2:对氨基苯磺酰胺(一种磺胺药)类似于对氨基苯甲酸(叶酸的组成部分),抑制二氢叶酸还原酶
(三)可逆抑制作用和不可逆抑制作用的鉴别
(四)一些重要的抑制剂
1、不可逆抑制剂:
(1)非专一性不可逆抑制剂:有机磷、汞、砷化合物;重金属盐、烷化剂、氰化物,硫化物和CO;青霉素;
(2)专一性不可逆抑制剂:
Ks型不可逆抑制剂:具有底物类似的结构,同时还带有一个活泼的化学基团可以修饰酶分子活性部位(称亲和标记试剂),但也能修饰其他部位的同一基团,故专一性有限。如TLCK是胰蛋白酶的~。
Kcat型不可逆抑制剂:有天然底物的类似结构,且本身也是酶的底物。抑制剂还有潜伏的反应基团,暴露或活化后可使酶不可逆失活,专一性极强。也称为 阕陨毙缘孜铩±。如β-卤代-D-Ala是细菌中丙氨酸消旋酶的~。
四、温度对酶反应的影响
酶促反应速度随温度升高而达到一最大值时的温度就称为酶的最适温度。
酶的最适温度与实验条件有关,因而它不是酶的特征性常数。
五、pH对酶反应的影响
观察pH对酶促反应速度的影响,通常为一“钟形”曲线,即pH过高或过低均可导致酶催化活性的下降。
在一定条件下,酶催化活性最高时溶液的pH值就称为酶的最适pH。
人体内大多数酶的最适pH在6.5~8.0之间。
酶的最适pH不是酶的特征性常数。
pH影响酶活力的原因可能有:
1、过酸、过碱会影响酶蛋白的构象,甚至使要酶变性而失活;
2、pH的改变导致了酶的催化基团以及底物分子的解离状态改变,影响酶活力或专一性。
六、激活剂对反应速度的影响
能够促使酶促反应速度加快的物质称为酶的激活剂(activator)。
酶的激活剂大多数是无机离子,如:K+、Na+、Mg2+、Ca2+、Cl- 、Br-;或有机小分子,如:Cys、GSH等。
本章重点:
酶反应动力学
知识点:
1、酶促反应的动力学(米氏学说、米氏常数、双倒数作图法、多种底物反应的不同机理、抑制剂对酶反应的影响);
2、酶的抑制作用;
3、酶反应的影响因素。
课后习题:P381-4,5,6,10
 爱华网
爱华网