假设检验是数理统计中按照一定的假设条件由样本推断总体的一种方法,因此假设检验也成为“显著性检验(Test of statisticalsignificant)”,是研究样本与样本之间、样本与总体之间的误差是由抽样误差引起的还是本质误差的统计推断方法。它的基本思想是在假设成立的条件下,根据某个统计方法(如Z检验、卡方检验等)的方法估计输入数据的统计特性,根据统计特性和输入数据的分布估计假设成立的概率大小,如果小于某一个预先设定的“显著性水平(significantlevel)”则说明假设不成立,反之则说明假设成立。假设检验所定义的假设成为零假设,数学上一般写成H0(念:H-nought)。与H0对立的假设,即对立假设,也称为备择假设。由于我们对于假设的判断是基于概率统计所作出的判断,那么我们就很有可能(一定的概率)做出错误的判断。错误分两种,第一类错误为H0假设成立,但是我们却认为它不成立,第二类错误是说H0不成立,但是我们却认为它成立。一般而言,第一类错误更难为人所忍受,所以在判断时,允许犯这种错误的可能性必须要极低——即犯第一类错的事件应该是一个小概率事件。假设检验就是基于这种小概率原理,即事先确定的作为判断的标准,即允许犯错的小概率标准,这种小概率标准就是统计学上定义的“显著性水平-α”,如果根据假设计算出来的概率小于这个显著性水平,则拒绝原假设,反之,如果大于这个标准,则承认原假设。因此,一般把1-α称为“置信区间”或者“接收区间”,小于α的区间称为“拒绝区间”。举个例子来说明,一个人被控诉犯罪,陪审团根据现有的条件做出对这个人有罪还是无罪的判断。事实上,陪审团就是进行一个假设检验。假设H0:被告无罪假设H1:被告有罪当然,陪审团现在还不知道哪个假设是成立的,他们必须根据控辩双方的证词做出判断,判断的结果只有两种,一种是被告无罪释放,一种是被告罪名成立。在判断的过程中,陪审团可能犯的错有两种,一种是被告本来无罪被判成有罪,一种是被告有罪却无罪释放。从司法的角度来看,第一类的错误更严重,因此我们的司法系统要求构建的第一类错误的概率尽可能小。假设检验的基本步骤:1、根据要研究解决的问题,提出原假设和备择假设:H0:假设样本与总体之间的误差是抽样误差引起的H1:假设样本与总体之间的误差是本质误差引起的2、选定可以允许的小概率标准,即假设H0成立却错误判断的可允许范围α;3、在假设的条件下,选择适当的统计方法,如卡方检验、Z检验、T检验等,计算出对应的统计量大小,如X2值,t值等;4、根据样本数据的分布和统计量的大小计算假设成立的概率大小,如果小于显著性水平,则拒绝原假设,如果大于等于显著性水平,则原假设成立。
爱华网本文地址 » http://www.aihuau.com/a/25101017/352243.html
更多阅读
原文地址:SAS中做蒙特卡洛模拟,根据已知对数正态分布,求符合该对数正态分布的随机数作者:庆可在SAS中没有直接产生对数正态分布随机数的函数。但是,我们可以通过以下公式转换来产生相应的对数正态分布随机数。例如:经检验以下数据经过检
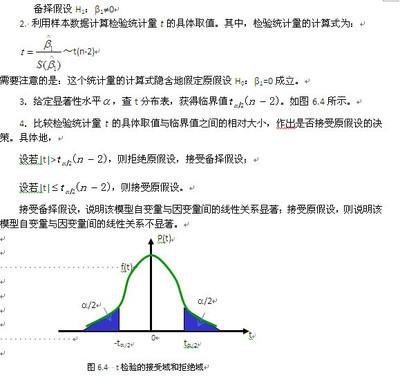
什么是Z检验Z检验是一般用于大样本(即样本容量大于30)平均值差异性检验的方法。它是用标准正态分布的理论来推断差异发生的概率,从而比较两个平均数的差异是否显著。当已知标准差时,验证一组数的均值是否与某一期望值相等时,用Z检验。
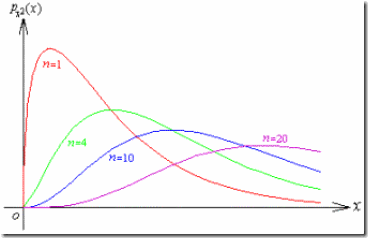
一、问题的提出 在科学研究或日常生活中,常常需要判断某一事物在同类事物中的好坏、优劣程度及其发展规律等问题。而影响事物的特征及其发展规律的因素(指标)是多方面的,因此,在对该事物进行研究时,为了能更全面、准确地反映出它的特征

这段时间又使用到cfa,给不是很懂cfa的自己留个记号: 我们有了一个理论模型,总想用数据来验证这个模型。收集、整理后就着手对数据进行cfa,常用的拟合指标是我们判断数据与理论模型的拟合程度的依据。常用的拟合指标:1.卡方:卡方的大小显示
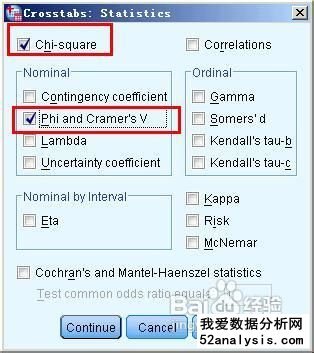
spss中交叉分析主要用来检验两个变量之间是否存在关系,或者说是否独立,其零假设为两个变量之间没有关系。在实际工作中,经常用交叉表来分析比例是否相等。例如分析不同的性别对不同的报纸的选择有什么不同。spss交叉表分析方法与步骤:







