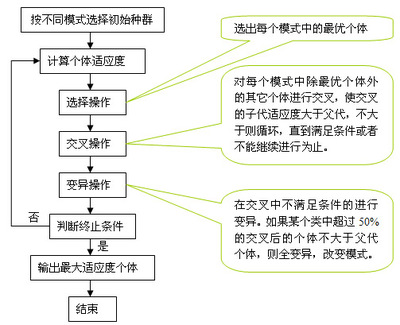
假设有一直径D1=20μm(半径r=10μm),高为100μm的圆柱体。由此存在一个与该圆柱体积相等球体的直径D2。我们可以这样计算这一直径(D2):圆柱体积V1=π×r2×h=1000π(μm3)------------------------------------ (2)
球体体积V2=4/3π×X3-----------------------------------------------------(3)在这里X表示等体积半径。因为圆柱体积V1=球体体积V2,所以
--------------(4)这样等效球体的直径D2=2X=2×19.5=39μm。就是说,一个高100μm,直径20μm的圆柱的等效球体直径大约为40μm。下面的表格列出了各种比率的圆柱体的等效球径。
圆柱尺寸 | 比率 | 等效球径 | |
| 高度 | 底面直径 | ||
| 20 40 100 200 400 10 4 2 | 20 20 20 20 20 20 20 20 | 1:1 2:1 5:1 10:1 20:1 1:2 1:5 1:10 | 22.9 28.8 39.1 49.3 62.1 18.2 13.4 10.6 |
--------------(5)在数学中,这样的数值通常称为D[1,0],因为在等式上方的直径各项是d1的幂,且在等式下方,没有直径项(d0)。
假设我是一名催化剂工程师,我想根据表面积来比较这些球体,因为表面积越大,催化剂作用就越大。一个球体的表面积是4πr2。因此,要根据表面积来比较,我们必须平方直径,而后被颗粒数量除,再开平方得到一个与面积有关的平均直径:
----------------------------- (6)这是一个数量-表面积平均值,它是将直径的平方相加后除以颗粒数量得到的,因此在数学中这样的数值被称为D[2,0],即分子是直径各项的平方和Σd2,分母无直径项(d0)。
如果我是一名化学工程师,我想根据重量来比较各球体。记得球体的重量是:
W=4/3π×r3×ρ---------------------------------------------------- (7)由式(7)可知,要得到与重量有关的平均径,必须用直径的立方除以颗粒数后再开立方。这是一个数量—体积或数量/重量平均值,它是将直径的立方相加后除以颗粒数量得到的,即分子是直径各项的立方和Σd3,分母为颗粒的数量,无直径项(d0)。在数学术语中这被称为D[3,0]。
------------ ----- (8)对于这些简单的平均值D[1,0],D[2,0],D[3,0],主要的问题是颗粒的数量是为公式所固有的,这就需要求出大量的颗粒的数量。通过简单的计算可以知道,在1克密度位2.5的二氧化硅粉体中,假设颗粒尺寸都是1μ,将会有大约760×109颗粒存在。如此巨大数量的颗粒数是无法准确测量的,所以无法用上述方法计算颗粒的各种平均径。因此引入动量平均的概念,两个最重要的动量平均径如下:这些平均径与惯性矩(惯性动量)相似,且在直径中引入另一个线性项(也就是说表面积与d3,体积及质量与d4有如下关系:
上述这些公式表明,(表面积或体积/质量的)分布围着频率的中点旋转。它们实际上是相应分布的重心。此种计算方法的优点是显而易见的:公式中不包含颗粒的数量,因此在不知晓相关颗粒数量的情况下,可以计算平均值及其分布。激光衍射最初计算了围绕着体积项为基础的分布,这也是D[4,3]以显著的方式报告的原因。
如果我们用电子显微镜测量粒子,这就像我们用十字线来量直径,把这些直径相加后被粒子数量除,得到一个平均结果。我们可以看到,用这种方法我们得到D[1,0],即长度平均值;如果我们得到颗粒的平面图像,通过测量每一颗粒的面积并将它们累加后除以颗粒数量,我们得到D[2,0],即面积平均径;如果采用一种比如电子区域感应的方法,我们就可以测量每一颗粒的体积,将所有颗粒的体积累加后除以颗粒的数量,我们得到D[3,0],即体积平均径。用激光法可以得到D[4,3],也叫体积平均径。如果粉体密度是恒定的,体积平均径与重量平均径是一致的。由于不同的粒度测试技术都是对粒子不同特性的测量,所以每一种技术都很会产生一个不同的平均径而且它们都是正确的。这就难免给人造成误解盒困惑。假设3个球体其直径分别为1,2,3个单位,那么不同方法计算出的平均径就大不相同:
数量及体积分布| 尺寸(cm) | 数量 | 数量 百分数 | 重量 百分数 |
| 10-1000 | 7000 | 0.2 | 99.96 |
| 1-10 | 17500 | 0.5 | 0.03 |
| 0.1-1 | 3500000 | 99.3 | 0.01 |
| 合计 | 3524500 | 100 | 100 |
| 表2颗粒大小数量与分布的影响 | |||
如果我们用电子显微镜测量颗粒,我们从前面的讨论知可以得到D[1,0]或叫做数量—长度平均径。如果我们确实需要质量或体积平均径,则我们必须将数量平均值转化成为质量平均值。以数学的角度来看,这是容易且可行的,但让我们来观察一下这种转换的结果。
假设我们的电子显微镜测量数量平均径时的误差为±3%,当我们把数量平均径转换成质量平均径时,由于质量是直径的立方函数,则最终质量平均径的误差为±27%。
但是如果我们像对激光衍射那样来计算质量或体积分布,则情况就不同了。对于被测量的在悬浮液中重复循环的稳定的样品,我们得出±0.5%重复性误差的体积平均径。如果我们将它转换为数量平均,则数量的平均径误差是0.5%的立方根,小于1.0%。在实际应用中,这意味着如果我们用电子显微镜且我们真正想得到的是体积或质量分布,则忽略或丢失1个10u粒子的影响与忽略或丢失1000个1u粒子的影响相同。由此我们必须意识到这一转换的巨大的危险。在MalvernSizers这种型号的仪器中,DOS系统与Windows软件都可计算其它导出的直径,但我们必须在怎样解释这些导出的直径方面很谨慎。依据以下的等式(Hatch-Choate转换)(参考7),不同的平均值可互相转换。(计算方法略)
我们已看到,Malvern激光衍射技术是分析光能数据来得出颗粒体积分布(对于弗朗和费理论,投影面积分布是假定的)。这一体积分布就像以上所列的那样可转换成任何一个数量或长度直径。
但是在任何一个分析方法中,我们必须意识到这种转换的结果(见上一段“数量,长度,体积/质量平均数之间的转换”)哪个平均径是由仪器实际测量的,哪些是由测量值导出的。相对于导出的直径,我们应更相信所测直径。实际上,在一些实例中,完全依靠导出数据是很危险的。例如,Malvern激光粒度仪以m2/cc或m2/kg的形式给出了比表面积。但对于该值我们不能太当真。如果我们确实需要得到物质的比表面积,那么我们就应该用直接测量比表面积的具体的方法,如B.E.T法等去直接测量。
每一个不同的粒度测量方法都是测量粒子的一个不同的特性(大小)。我们可以根据多种不同的方法得到不同的平均结果(如D[4,3],D[3,2]等),那么我们应该用什么数字呢?让我们举一个简单的例子,两个直径分别为1和10的球体,对冶金行业,如果我们计算简单的数字平均直径,我们得到的结果是:D(1,0)=(1+10)/2=5.5。但是如果我们感兴趣的是物质的质量,我们知道,质量是直径的三次函数,我们就发现直径为1的球体的质量为1,直径为10的球体的质量为1000。也就是说,大一些的球体占系统总质量的1000/1001。在冶金上我们可以丢掉粒径为1的球体,这样我们只会损失总质量的0.1%。因此简单的数字平均不能精确的反映系统的质量,用D[4,3]能更好地反映颗粒地平均质量。
在我们上述的两个球体例子中,质量或体积动量平均径计算如下:
该值能比较充分地表示系统的质量更多的存在哪里,这对一些行业非常重要。但是对于一间制造大规模集成电路的洁净的屋子来说,颗粒的数量或浓度就是最重要的了,一个颗粒落在硅片上,就将会产生一个疵点。这时我们就要采用一种方法直接测量粒子的数量或浓度。从本质上说,这是颗粒计数与测量颗粒大小之间的区别。对于颗粒计数来说,我们记录下每一个颗粒并且点出数量就可以了,颗粒的大小不太重要;对于测量颗粒大小来说,颗粒的大小或分布是我们关心的,颗粒的绝对数量并不重要。
定义这三个术语是很重要的,它们在统计及粒度分析中常常被用到。
平均径:这是表示颗粒平均大小的数据。有很多不同的平均值的算法,如D[4,3]等。
中值:也叫中位径或D50,这是一个表示粒度大小的典型值,该值准确地将总体划分为二等份,也就是说有50%的颗粒超过此值,有50%的颗粒低于此值。
最频值:这是频率分布的最通用的值,也就是说频率曲线的最高点。设想这是一般的分布或高斯分布。则平均值,中值和最频值将恰好处在同一位置,如图4。但是,如果这种分布是如图5所示的双峰分布。则平均直径几乎恰恰在这两个峰的中间。实际上并不存在具有该粒度的颗粒。中值直径将位于偏向两个分布中的较高的那个分布1%,因为这是把分布精确地分成二等份的点。最频值将位于较高曲线的顶部。由此可见,平均值、中值和最频值有时是相同的,有时是不同的,这取决于样品的粒度分布的形态。注意,在Malvern分析表中:
从以前几段中我们看到,每一种测量技术都将的到不同的结果,因为它测量该颗粒的不同方面。我们现在讨论当前应用的几种不同测量方法的相对的优缺点。
筛分法这是一种古老的方法,其优点是成本低,使用容易等。T.艾伦在《颗粒大小测定》一书中讨论了重复筛分方面的困难,对于很多用户来说筛分法的主要缺点如下:
沉降法这是在油漆及陶瓷等工业中应用的一种传统的测量方法,这种测量的原理是以Stokes定律为基础:
该类设备有象移液管一类的简单的装置,也有带离心机或以X射线做光源的复杂一些的装置。
对等式18的研究我们可以发现它的缺陷:它需要知道物质的密度,因而这种方法对乳浊液不适合,因为在乳浊液中物质不沉淀,或者密度较大的颗粒沉淀得很快。最终结果是一个与重量直径(D[4,3])不同的Stokes直径(DST),且只是具有相同沉淀率的颗粒与球体的比较。在分母中的粘度项表明我们须精确地控制温度变化,温度改变1℃,粘度将会改变2%。
这一等式可容易地计算出沉降时间。可以看出,在20℃的水中,1微米的SiO2颗粒(密度为2.5)在重力的作用下要经过3.5小时沉淀1厘米。因而该测量进行得很缓慢且还要面临乏味的重复测量。因此考虑到增大g以尽量补救这一缺点。在参考3中讨论了关于增大g的不利条件。关于沉降方法更多具体的批评见参考2。Stokes定律仅适用于那些具有一定特性的球体,这些特性是:这些球体相对于其体积或表面积具有最紧凑的形状。而具有不规则形状的普通粒子的表面积比球体的表面积大,因而增加了阻力而比他们的等效球体沉降得更慢。布朗运动位移与重力沉降位移比较(见下表):
| 在1秒内的位移(微米) | ||||||
| 粒径 | 在华氏70度空气中(标准大气压) | 在华氏70度水中 | 在华氏70度空气中 | |||
| 由于布朗运动 | 由于重力 | 由于布朗运动 | 由于重力 | r | K=100r(%) | |
| 0.10 0.25 0.50 1.00 2.50 10.0 | 29.4 14.2 8.92 5.91 3.58 1.75 | 1.73 6.30 19.9 69.6 400 1550 | 2.36 1.49 1.052 0.745 0.334 0.236 | 0.005 0.0346 0.1384 0.554 13.84 55.4 | 31.1 3.15 0.556 0.0983 0.00995 0.00031 | 96.9 75.9 35.7 5.0 1.0 0.03 |
布朗运动位移与重力沉降位移比较
对于像高岭土那样呈圆盘形状的物体,情况就更为严重,实际相比会产生很大的偏差。另外对于小的颗粒来说,同时存在重力沉降与布朗运动两种运动状态。由上方的表格列出了这两种运动状态的对比可知,如果用沉降法测量小于2um的颗粒,我们会看到很大的误差(大约为20%)并且对于0.5um的颗粒来说,误差甚至会超过100%。沉降法的缺点如下:
这种技术在20世纪50年代中期发明的,最早用来测量血球的大小。这些血球实际上是呈单模态悬浮在稀释的电解溶液中。此法原理很简单。在电解溶液中放置一个有小孔的玻璃器皿,使稀释的悬浮液流过该小孔,在小孔两端施加电压。当粒子流过孔洞时,电阻发生了变化,产生电压脉冲。在仪器上测量该脉冲的峰值的高度,然后与标准颗粒的脉冲峰高比较,从而得到被测颗粒的大小。因此这种方法不是一个绝对的方法,它是有比较性质的。对于血球而言,此种方法是最好不过的,它能得出数量及体积分布,对于工业材料来说此法则存在着如下缺陷:
显微镜检测法这是一个很好的方法,因为它使人们得以直接观察颗粒的形状,并可以据此判断分散的效果是否良好或者颗粒有无聚合现象。有趣的是1g密度为2.5,粒度为10μm的粒子竟含有760×106个颗粒,这么多的颗粒我们不可能用显微镜一个一个地单独观察它们。
但是,当质量或生产控制仅仅依赖上述的简单判断,这是不合适的。相对来说,我们仅可以观察到很少的颗粒,如果以这种非代表性的结果为依据确实是很危险的。另外,如果测量重量分布则误差会更大,因为忽略1个10μm的粒子与忽略1千个1μm的粒子产生的影响是一样的。
电子显微镜有着复杂的样品制备,因此很慢。人工操作的显微镜,只能观察到为数很少的颗粒(一个优秀的操作人员一天大约可以观察2000个颗粒)。但操作人员极易疲劳,这又是“要测量哪一方面?”的问题了。所以在测量同一样品时操作者与操作者之间的变化性很大。对颗粒的形状表征来说,显微镜检测法仍不失为一个有用的帮助。
称之为小角度激光散射(LALLS)会更准确。在很多表征及质量控制工业中,此法已经成为首选的粒度测试方法。根据ISO13320其应用范围是0.1—3000μm。在过去的大约20多年里,在这一领域中,该仪器也有了长足的发展。这种方法依据这一现象:衍射角与粒度成反比。该仪器包括如下部件:
落后一些的设备及现在的仪器都只依据弗朗和费近似法,此法假设:
- 粒子比所应用的光的波长大许多(ISO13320将此定义为大于40λ,也就是,当使用He-Ne激光器时大25μm)。
- 所有颗粒的散射效率相等。
- 颗粒是不透明的而且不会传导光。
这些假设对于很多物质永远都是不正确的。对于小的颗粒会增大误差,以至于接近30%,特别是物质与介质的相对折射率接近于1且粒度接近光波长度时,散射就变成了存在最大值与最小值之间的复杂函数。最新式的仪器(如Malvern生产的Mastersize2000仪器)充分地利用了米氏理论解了光与物质之间相互作用的方程。这使得在很大的粒度范围内,测试结果都很精确(典型的是0.02—2000μm)。米氏理论与费氏理论不一样,它把颗粒的体积假想为所预测的投影面积。这种方法虽然精确但缺点是须知道物质及介质的折射率,并且应知道或者猜出折射率中的吸收部分。但对于大多数用户来说,这不会带来困难,因为这些值已为人们普遍了解或可测量出来。
激光衍射为最终用户提供了以下优点:
- 参考书目:
- 油漆及表面涂层—理论与实践;Ed.R.Lambourne Ellis Horwood.有限公司1993年出版。ISBN0-13-030974-5PGk
- 粒度测试:T.Allen, Chapman&Hall.公司1992年第四版。ISBN04123570
- G.JJ.Beckers,H. J. Veringa公司;粉体技术 60 (1989)245-248页。
- J. Ranucci 制药技术;1992年10月出版,第108-114页。
- G.Hind; 制造业化学家;1990年,28-30页。
- M .W. Wedd; ILASS-欧洲第八届年会,1992年9月30日—10月2日阿姆斯特丹。
- T. Hatch & S.P Choate. J. Franklin学会。1929年369-387页。
- Malvern分公司:英国公司 法国公司 美国公司 德国公司 马来西亚公司 瑞典公司 以密度为基础的。
 爱华网
爱华网