简单的遗传算法实例 多目标遗传算法实例

遗传算法的概念最早是由Bagley J.D于1967年提出的。后来Michigan大学的J.H.Holland教授于1975年开始对遗传算法（GeneticAlgorithm,GA）的机理进行系统化的研究。遗传算法是对达尔文生物进化理论的简单模拟，其遵循“适者生存”、“优胜略汰”的原理。遗传算法模拟一个人工种群的进化过程，并且通过选择、杂交以及变异等机制，种群经过若干代以后，总是达到最优（或近最优）的状态。

自从遗传算法被提出以来，其得到了广泛的应用，特别是在函数优化、生产调度、模式识别、神经网络、自适应控制等领域，遗传算法更是发挥了重大的作用，大大提高了问题求解的效率。遗传算法也是当前“软计算”领域的重要研究课题。

本文首先结合MATLAB对遗传算法实现过程进行详细的分析，然后通过1个实际的函数优化案例对其应用进行探讨。

1. 遗传算法实现过程

现实生活中很多问题都可以转换为函数优化问题，所以本文将以函数优化问题作为背景，对GA的实现过程进行探讨。大部分函数优化问题都可以写成求最大值或者最小值的形式，为了不是一般性，我们可以将所有求最优值的情况都转换成求最大值的形式，例如，求函数f(x)的最大值，

若是求函数f(x)的最小值，可以将其转换成g(x)=-f(x)，然后求g(x)的最大值，

这里x可以是一个变量，也可是是一个由k个变量组成的向量,x=(x₁, x₂, …,x_k)。每个x_i, i=1,2,…,k,其定义域为D_i，D_i=[a_i,b_i]。

一般规定f(x)在其定义域内只取正值，若不满足，可以将其转换成以下形式，

其中C是一个正常数。

1.1 编码与解码

要实现遗传算法首先需要弄清楚如何对求解问题进行编码和解码。对于函数优化问题，一般来说，有两种编码方式，一是实数编码，一是二进制编码，两者各有优缺点，二进制编码具有稳定性高、种群多样性大等优点，但是需要的存储空间大，需要解码过程并且难以理解；而实数编码直接用实数表示基因，容易理解并且不要解码过程，但是容易过早收敛，从而陷入局部最优。本文以最常用的二进制编码为例，说明遗传编码的过程。

从遗传算法求解的过程来看，需要处理好两个空间的问题，一个是编码空间，另一个是解空间，如下图所示

从解空间到编码空间的映射过程成为编码过程；从编码空间到解空间的映射过程成为解码过程。下面就以求解一个简单的一维函数f(x) =-(x-1)^2+4, x的取值范围为[-1,3]最大值为例，来说明编码及解码过程。

编码：

在编码之前需要确定求解的精度，在这里，我们设定求解的精度为小数点后四位，即1e-4。这样可以将每个自变量x_i的解空间划分为个等分。以上面这个函数为例，即可以将x的解空间划分为(3-(-1))*1e+4=40000个等分。使n_i满足，这里n_i表示使上式成立的最小整数，即表示自变量x_i的基因串的长度。因为2¹⁵<40000<2¹⁶，这里n_i取16。例如0000110110000101就表示一个解空间中的基因串。表示所有自变量x=(x₁,x₂, …,x_k)的二进制串的总长度称为一个染色体(Chromosome)的长度或者一个个体(Individual)的长度，。编码过程一般在实现遗传算法之前需要指定。

解码：

解码即将编码空间中的基因串翻译成解空间中的自变量的实际值的过程。对于二进制编码而言，每个二进制基因串都可以这样翻译成一个十进制实数值，。例如基因串0000110110000101，可以翻译为，这里二进制基因串转变成十进制是从左至右进行的。

1.2 初始化种群

在开始遗传算法迭代过程之前，需要对种群进行初始化。设种群大小为pop_size，每个染色体或个体的长度为chromo_size，种群的大小决定了种群的多样性，而染色体的长度则是由前述的编码过程决定的。一般随机生成初始种群，但是如果知道种群的实际分布，也可以按照此分布来生成初始种群。假设生成的初始种群为(v₁,v₂, …, v_{pop_size})。

1.3 选择操作

选择操作即从前代种群中选择个体到下一代种群的过程。一般根据个体适应度的分布来选择个体。以初始种群(v₁,v₂, …,v_{pop_size})为例，假设每个个体的适应度为(fitness(v₁),fitness(v₂),…,fitness(v_{pop_size}))，一般适应度可以按照解码的过程进行计算。以轮盘赌的方式选择个体，如下图

随机转动一下轮盘，当轮盘停止转动时，若指针指向某个个体，则该个体被选中。很明显，具有较高适应度的个体比具有较低适应度的个体更有机会被选中。但是这种选择具有随机性，在选择的过程中可能会丢失掉比较好的个体，所以可以使用精英机制，将前代最优个体直接选到下一代中。

轮盘赌选择具体算法如下（这里假定种群中个体是按照适应度从小到大进行排列的，如果不是，可以按照某种排序算法对种群个体进行重排）：

Selection Algorithmvar pop, pop_new;var fitness_value, fitness_table;for i=1:pop_size    r = rand*fitness_table(pop_size);        first = 1;            last = pop_size;            mid = round((last+first)/2);            idx = -1;                    while (first <= last) && (idx == -1)                 if r > fitness_table(mid)                    first = mid;                elseif r < fitness_table(mid)                    last = mid;                     else                    idx = mid;                    break;                end if                mid = round((last+first)/2);                if (last - first) == 1                    idx = last;                    break;                end if           end while              for j=1:chromo_size                pop_new(i,j)=pop(idx,j);           end forend forif elitism        p = pop_size-1;else        p = pop_size;end iffor i=1:p       for j=1:chromo_size            pop(i,j) = pop_new(i,j);       end forend for

1.3 交叉操作

交叉操作是对任意两个个体进行的（在这里我们实现的算法是直接对相邻的两个个体进行的）。随机选择两个个体，如下图所示

然后随机生成一个实数0<=r<=1, 如果r

单点交叉具体算法如下：

Crossover algorithmfor i=1:2:pop_size            if(rand < cross_rate)                cross_pos = round(rand * chromo_size);                if or (cross_pos == 0, cross_pos == 1)                    continue;                end if                for j=cross_pos:chromo_size                    pop(i,j)<->pop(i+1,j);                end for            end ifend for

1.4 变异操作

变异操作是对单个个体进行的。首先生成一个随机实数0<=r<=1, 如果r

如个体需要进行变异操作，首先需要确定变异位置(rand*chromo_size)，若为0则不进行变异，否则则对该位置的二进制数字进行变异：1变成0,0变成1.（当然也可以选择多点进行变异）

单点变异的具体算法描述如下：

Mutation algorithmfor i=1:pop_size            if rand < mutate_rate                mutate_pos = round(rand*chromo_size);                if mutate_pos == 0                    continue;                end if                pop(i,mutate_pos) = 1 - pop(i, mutate_pos);            end ifend for

1.5 遗传算法流程

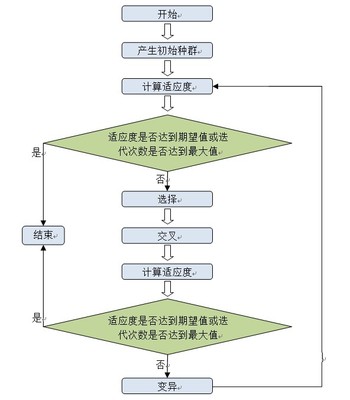
遗传算法计算流程图如下图所示

1.6 MATLAB程序实现

初始化：

%初始化种群%pop_size: 种群大小%chromo_size: 染色体长度function initilize(pop_size, chromo_size)global pop;for i=1:pop_size    for j=1:chromo_size        pop(i,j) = round(rand);    endendclear i;clear j;

计算适应度：（该函数应该根据具体问题进行修改，这里优化的函数是前述的一维函数）

%计算种群个体适应度，对不同的优化目标，此处需要改写%pop_size: 种群大小%chromo_size: 染色体长度function fitness(pop_size, chromo_size)global fitness_value;global pop;global G;for i=1:pop_size    fitness_value(i) = 0.;    endfor i=1:pop_size    for j=1:chromo_size        if pop(i,j) == 1            fitness_value(i) = fitness_value(i)+2^(j-1);        end            end     fitness_value(i) = -1+fitness_value(i)*(3.-(-1.))/(2^chromo_size-1);     fitness_value(i) = -(fitness_value(i)-1).^2+4;endclear i;clear j;

对个体按照适应度大小进行排序：

%对个体按适应度大小进行排序，并且保存最佳个体%pop_size: 种群大小%chromo_size: 染色体长度function rank(pop_size, chromo_size)global fitness_value;global fitness_table;global fitness_avg;global best_fitness;global best_individual;global best_generation;global pop;global G;for i=1:pop_size        fitness_table(i) = 0.;endmin = 1;temp = 1;temp1(chromo_size)=0;for i=1:pop_size    min = i;    for j = i+1:pop_size        if fitness_value(j)end    end    if min~=i        temp = fitness_value(i);        fitness_value(i) = fitness_value(min);        fitness_value(min) = temp;        for k = 1:chromo_size            temp1(k) = pop(i,k);            pop(i,k) = pop(min,k);            pop(min,k) = temp1(k);        end    end    endfor i=1:pop_size    if i==1        fitness_table(i) = fitness_table(i) + fitness_value(i);        else        fitness_table(i) = fitness_table(i-1) + fitness_value(i);    endendfitness_tablefitness_avg(G) = fitness_table(pop_size)/pop_size;if fitness_value(pop_size) > best_fitness    best_fitness = fitness_value(pop_size);    best_generation = G;    for j=1:chromo_size        best_individual(j) = pop(pop_size,j);    endendclear i;clear j;clear k;clear min;clear temp;clear temp1;

选择操作：

%轮盘赌选择操作%pop_size: 种群大小%chromo_size: 染色体长度%cross_rate: 是否精英选择function selection(pop_size, chromo_size, elitism)global pop;global fitness_table;for i=1:pop_size    r = rand * fitness_table(pop_size);    first = 1;    last = pop_size;    mid = round((last+first)/2);    idx = -1;    while (first <= last) && (idx == -1)         if r > fitness_table(mid)            first = mid;        elseif r < fitness_table(mid)            last = mid;             else            idx = mid;            break;        end        mid = round((last+first)/2);        if (last - first) == 1            idx = last;            break;        end   end      for j=1:chromo_size        pop_new(i,j)=pop(idx,j);   endendif elitism    p = pop_size-1;else    p = pop_size;endfor i=1:p   for j=1:chromo_size        pop(i,j) = pop_new(i,j);   endendclear i;clear j;clear pop_new;clear first;clear last;clear idx;clear mid;

交叉操作：

%单点交叉操作%pop_size: 种群大小%chromo_size: 染色体长度%cross_rate: 交叉概率function crossover(pop_size, chromo_size, cross_rate)global pop;for i=1:2:pop_size    if(rand < cross_rate)        cross_pos = round(rand * chromo_size);        if or (cross_pos == 0, cross_pos == 1)            continue;        end        for j=cross_pos:chromo_size            temp = pop(i,j);            pop(i,j) = pop(i+1,j);            pop(i+1,j) = temp;        end    endendclear i;clear j;clear temp;clear cross_pos;

变异操作：

%单点变异操作%pop_size: 种群大小%chromo_size: 染色体长度%cross_rate: 变异概率function mutation(pop_size, chromo_size, mutate_rate)global pop;for i=1:pop_size    if rand < mutate_rate        mutate_pos = round(rand*chromo_size);        if mutate_pos == 0            continue;        end        pop(i,mutate_pos) = 1 - pop(i, mutate_pos);    endendclear i;clear mutate_pos;

打印算法迭代过程：

%打印算法迭代过程%generation_size: 迭代次数function plotGA(generation_size)global fitness_avg;x = 1:1:generation_size;y = fitness_avg;plot(x,y)

算法主函数：

%遗传算法主函数%pop_size: 输入种群大小%chromo_size: 输入染色体长度%generation_size: 输入迭代次数%cross_rate: 输入交叉概率%cross_rate: 输入变异概率%elitism: 输入是否精英选择%m: 输出最佳个体%n: 输出最佳适应度%p: 输出最佳个体出现代%q: 输出最佳个体自变量值function [m,n,p,q] = GeneticAlgorithm(pop_size, chromo_size, generation_size, cross_rate, mutate_rate, elitism)global G ; %当前代global fitness_value;%当前代适应度矩阵global best_fitness;%历代最佳适应值global fitness_avg;%历代平均适应值矩阵global best_individual;%历代最佳个体global best_generation;%最佳个体出现代fitness_avg = zeros(generation_size,1);disp "hhee"fitness_value(pop_size) = 0.;best_fitness = 0.;best_generation = 0;initilize(pop_size, chromo_size);%初始化for G=1:generation_size       fitness(pop_size, chromo_size);  %计算适应度     rank(pop_size, chromo_size);  %对个体按适应度大小进行排序    selection(pop_size, chromo_size, elitism);%选择操作    crossover(pop_size, chromo_size, cross_rate);%交叉操作    mutation(pop_size, chromo_size, mutate_rate);%变异操作endplotGA(generation_size);%打印算法迭代过程m = best_individual;%获得最佳个体n = best_fitness;%获得最佳适应度p = best_generation;%获得最佳个体出现代%获得最佳个体变量值，对不同的优化目标，此处需要改写q = 0.;for j=1:chromo_size    if best_individual(j) == 1            q = q+2^(j-1);    end endq = -1+q*(3.-(-1.))/(2^chromo_size-1);clear i;clear j;

2. 案例研究

对上一节中的函数进行优化，设置遗传算法相关参数，程序如下

function run_ga()elitism = true;%选择精英操作pop_size = 20;%种群大小chromo_size = 16;%染色体大小generation_size = 200;%迭代次数cross_rate = 0.6;%交叉概率mutate_rate = 0.01;%变异概率[m,n,p,q] = GeneticAlgorithm(pop_size, chromo_size, generation_size, cross_rate, mutate_rate,elitism);disp "最优个体"mdisp "最优适应度"ndisp "最优个体对应自变量值"qdisp "得到最优结果的代数"pclear;

结果如下：

"最优个体"

m =

1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0

"最优适应度"

n =

4.0000

"最优个体对应自变量值"

q =

1.0000

"得到最优结果的代数"

p =

74

此结果非常准确。

算法迭代过程图形：

从上图中可以看出，随着迭代次数的增加，算法逐渐收敛。

3. 总结

本文详细的介绍了简单遗传算法的实现过程，并以一个简单的函数优化作为案例说明了其应用。但是由于该测试函数过于简单，在实际的应用过程中，还需要对相关参数进行调整，使其效率得到更大的提高。

转载于http://www.cnblogs.com/biaoyu/archive/2011/12/03/2274604.html

爱华网本文地址 » http://www.aihuau.com/a/25101017/359457.html