http://iask.sina.com.cn/b/2459822.html
http://hyz0.blog.sohu.com/69610635.html
http://baike.baidu.com/view/148250.htm
http://baike.baidu.com/view/148250.htm(百度上的这个有托勒密定理的推广,很有意思!)
一般几何教科书中的“托勒密定理”,实出自依巴谷(Hipparchus)之手,托勒密只是从他的书中摘出。
托勒密(Ptolemy)定理指出,圆内接凸四边形两对对边乘积的和等于两条对角线的乘积。
原文:圆内接四边形中,两对角线所包矩形的面积等于 一组对边所包矩形的面积与另一组对边所包矩形的面积之和。
从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式,托勒密定理实质上是关于共圆性的基本性质.(具体的推导方法详见数学目录下的博文《两角和与差的三角函数公式的证明》,利用托勒密定理这一思路来自网友的提供,我原来的证明用了另一种思路,但不如用托勒密定理来得简洁!)
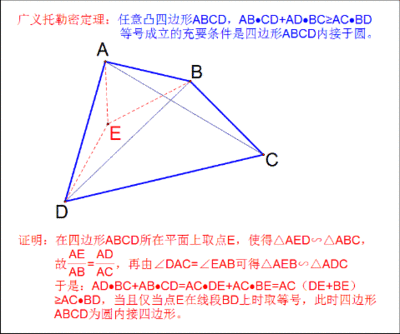
思路:托勒密定理在平面几何中赫赫有名,其难点在于:把一条对角线分割成两条线段DE和BE。第一步证明一对旋转的三角形相似:△ABE∽△ACD;第二步还需要证一对旋转的三角形相似△ADE∽△ACB;只有这两对相似的三角形出来了才能得到结论。
证明:以AB为边,作一个角等于已知角:即∠BAE=∠DAC;
在ΔABE和ΔACD中,
∵ ∠BAE=∠DAC;
∠ABE=∠ACD;
∴ △ABE∽△ACD;
∴AB·DC=BE·AC①
∵ ∠BAE=∠DAC;
∴ ∠DAE=∠CAB;
在ΔADE和ΔACB中,
∵ ∠ADE=∠ACB;
∠DAE=∠CAB;
∴ △ADE∽△ACB;
∴AD·BC=DE·AC②
∴ ①+②得:
AB·DC+ AD·BC= BE·AC+ DE·AC=(BE+DE)·AC=BD·AC。
结论:该命题对于圆内接的任意四边形都成立。最初是由数学家托勒密想出来的,叫做托勒密定理。“当你遇到AB·DC+AD·BC=AC·BD这样的等积式时,如果等式左边可以合二为一,则考虑证一对三角形相似,否则,在AC、BD的其中一条线段上找到一个分点,构造两个三角形相似。
-----------------------------------------------------------------------------------
推论
1.任意凸四边形ABCD,必有AC·BD≤AB·CD+AD·BC,当且仅当ABCD四点共圆时取等号。
2.托勒密定理的逆定理同样成立:一个凸四边形两对对边乘积的和等于两条对角线的乘积,则这个凸四边形内接于一圆。
证明
(以下是推论的证明,托勒密定理可视作特殊情况。)
在任意四边形ABCD中,作△ABE使∠BAE=∠CAD ∠ABE=∠ ACD
因为△ABE∽△ACD
所以 BE/CD=AB/AC,即BE·AC=AB·CD (1)
又有比例式AB/AC=AE/AD
而∠BAC=∠DAE
所以△ABC∽△AED相似.
BC/ED=AC/AD即ED·AC=BC·AD (2)
(1)+(2),得
AC(BE+ED)=AB·CD+AD·BC
又因为BE+ED≥BD
(仅在四边形ABCD是某圆的内接四边形时,等号成立,即“托勒密定理”)
所以命题得证
推广
托勒密不等式:四边形的任两组对边乘积不小于另外一组对边的乘积,取等号当且仅当共圆或共线。
简单的证明:复数恒等式:(a-b)(c-d)+(a-d)(b-c)=(a-c)(b-d),两边取模,
得不等式AC·BD≤|(a-b)(c-d)|+|(b-c)(a-d)|=AB·CD+BC·AD
注意:
1.等号成立的条件是(a-b)(c-d)与(a-d)(b-c)的辐角相等,这与A、B、C、D四点共圆等价。
2.四点不限于同一平面。
欧拉定理:在一条线段上AD上,顺次标有B、C两点,则AD·BC+AB·CD=AC·BD
 爱华网
爱华网