向量a·向量b=|a||b|cos<a,b>
在物理学中,已知力与位移求功,实际上就是求向量F与向量s的内积,即要用点乘。
将向量用坐标表示(三维向量),
若向量a=(a1,b1,c1),向量b=(a2,b2,c2),
则
向量a·向量b=a1a2+b1b2+c1c2
点乘可用于判断向量垂直
判断条件: 在向量a与向量b的模皆不为0的情况下,向量a·向量b=0 由向量a·向量b=|a||b|cos<a,b>可很容易的得出 当|a| 、|b|皆不为0时,cos<a,b>为0 也即向量a与向量b互相垂直。关于用点乘判断向量平行的误区
判断平行: 向量a·向量b=|a|*|b|; 而非向量a·向量b=1(×) 由向量a·向量b=|a||b|cos<a,b>可很容易的得出叉乘crossproduct
|向量c|=|向量a×向量b|=|a||b|sin<a,b>
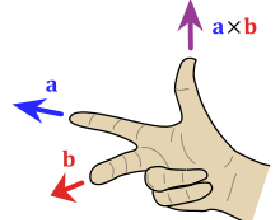
向量c的方向与a,b所在的平面垂直,且方向要用“右手法则”判断(用右手的四指先表示向量a的方向,然后手指朝着手心的方向摆动到向量b的方向,大拇指所指的方向就是向量c的方向)。
因此
向量的外积不遵守乘法交换率,因为向量a×向量b= -向量b×向量a
在物理学中,已知力与力臂求力矩,就是向量的外积,即叉乘。
将向量用坐标表示(三维向量),
若向量a=(a1,b1,c1),向量b=(a2,b2,c2),
则
向量a×向量b=
| i j k |
|a1 b1 c1|
|a2 b2 c2|
=(b1c2-b2c1,c1a2-a1c2,a1b2-a2b1)
(i、j、k分别为空间中相互垂直的三条坐标轴的单位向量)。
 爱华网
爱华网



