连通图 任何情况下的连通图

到这里，收集到的吉林大学的5个研究生机试题目就已经写完了。接下来写那个学校的好呢？看心情了！

题目描述

给定一个无向图和其中的所有边，判断这个图是否所有顶点都是连通的。

输入

每组数据的第一行是两个整数 n 和 m（0<=n<=1000）。n表示图的顶点数目，m 表示图中边的数目。如果 n 为 0 表示输入结束。随后有 m 行数据，每行有两个值 x 和y（0<x, y <=n），表示顶点 x 和 y 相连，顶点的编号从 1开始计算。输入不保证这些边是否重复。

输出

对于每组输入数据，如果所有顶点都是连通的，输出"YES"，否则输出"NO"。

样例输入

4 31 22 33 23 21 22 30 0

样例输出

NOYES

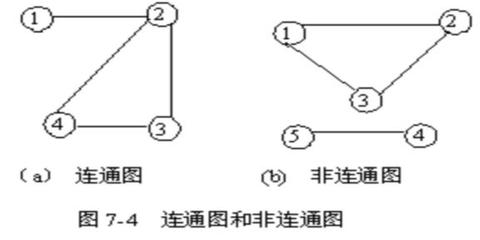
//首先，我觉得有必要温习一下图的连通性的相关概念
// I无向图G的连通性：
//若无向图G中的任何两个结点都是可达的，则称G是连通图(connected graph)，
//否则称G是非连通图(unconnected graph)或分离图(separated graph)
// II有向图G的连通性：
//若将有向图G所有边的方向略去，得无向图G'

//若G'是连通图则成G是连通图或弱连通图(weakly connected graph),否则为非连通图
//若G中任何一对结点间至少有一个结点是可达的，则成G是单向连通图(unilaterally connected graph)
//若G中任何一对结点之间都是相互可达的，则称G是强连通图(strongly connected graph)
//G是强连通图的充要条件是:G中存在一条经过所有结点的回路
//

//Dijkstra算法可用于解决一个点与其他点之间的最短路径问题,时间复杂度为O(n*n)
//Floyd算法是利用二维矩阵解决任意两个节点间的最短路径问题，时间复杂度为O(n*n*n)
// 鉴于Floyd算法中利用了二维矩阵，算法也相对而言易于实现，这里采用Floyd算法
//
// 实际上用Dijkstra算法就足够了，我们只需要判定一个节点V0到其余各节点Vi是否可达
// 如果可达必然就是连通图,因为既然V0可以达到各节点Vi

// 那么任何一个节点必然可以以V0为跳板到其他各节点
// 在用Floyd算法处理长度矩阵后，我们可以利用这个思想来检验V0到其余节点是否可达来验证无向图的连通性
// Dijkstra算法的实现方式

#include<iostream>
using namespace std;

#define MAX 50//图的节点数最大值，懒得设成1000了，我才懒得输入那么多数据呢
#define INFINITE 10000//设定两点间不可达的标识

//根据输入的边的信息更新长度矩阵数据
void Process(int d[][MAX],int v1,int v2);
//实现Floyd算法的函数了,d为长度矩阵，n为节点数目
void Floyd(int d[][MAX],int n);
//判断无向图G是否可达
bool Connected(int d[][MAX],int n);
//写个Floyd的一部分就可以解决问题，实际复杂度为O(n*n)
void Floyd1(int d[][MAX],int n);

int main()
{
int d[MAX][MAX];//长度矩阵
// 二维矩阵实际上也是地址连续的,对其进行初始化
memset(d,INFINITE,MAX*MAX);
int n;//节点数目
int m;//边的数目
cout<<"Input thenumber of vertex and edges:";
cin>>n;
while(n)
{
//其实这里不设置对角线的值也可以判断图的连通性,只是求出的最短路径是错的
for(intt=0;t<n;++t) d[t][t]=0;
cin>>m;
int v1,v2;//两个节点
cout<<"Inputthe two vertexes of each edge:";
for(inti=0;i<m;++i)
{
cin>>v1>>v2;
Process(d,v1,v2);
}
//下面一行替换成Floyd1照样可以正常运行出结果
Floyd(d,n);//运用Floyd算法处理长度矩阵
if(Connected(d,n))cout<<"Yes"<<endl;
elsecout<<"No"<<endl;
cout<<"Inputthe number of vertex:";
cin>>n;
}
return 0;
}

//根据输入的边的信息更新长度矩阵数据
void Process(int d[][MAX],int v1,int v2)
{
if(v1<=0||v2<=0)return;//节点数据必须大于0，否则不做任何处理
d[v1-1][v2-1]=d[v2-1][v1-1]=1;//1表示结点间可达
}

void Floyd(int d[][MAX],int n)
{
int tmp;
//时间复杂度为O(n*n*n)
for(int i=0;i<n;++i)
for(intj=0;j<n;++j)
for(intk=0;k<n;++k)
{
tmp=d[i][k]+d[k][j];
if(tmp<d[i][j])d[i][j]=tmp;
}
}

//判断无向图G是否可达
bool Connected(int d[][MAX],int n)
{
bool test=true;
for(inti=0;i<n&&test;++i)
if(d[0][i]>=INFINITE)test=false;
return test;
}

//Dijkstra算法我就不写了，实际写个Floyd的一部分就可以求出图的连通性，反正不用求出最短路径
void Floyd1(int d[][MAX],int n)
{
int tmp;
//时间复杂度为O(n*n)
for(int j=0;j<n;++j)
{
if(d[0][j]<INFINITE)continue;//节点间已经可达
for(intk=0;k<n;++k)
{
tmp=d[0][k]+d[k][j];
if(tmp<d[0][j])d[0][j]=tmp;
}
}
}

爱华网本文地址 » http://www.aihuau.com/a/25101017/367423.html