多项式回归分析 指数回归模型的应用

三、多项式回归

1、一元多项式回归函数

y=a1xm+a2xm-1+....+amx+am+1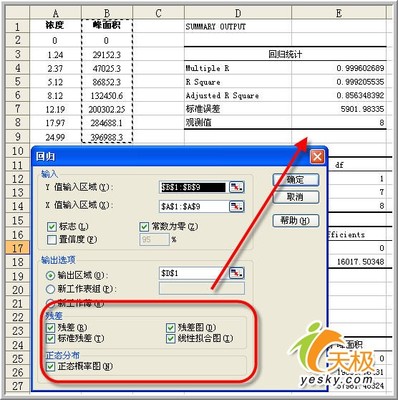


(1)[p,S]=polyfit(x,y,m) 确定多项式系数的MATLAB命令
说明：x=(x1,x2,…,xn),y=(y1,y2,…,yn)；p=(a1,a2,…,am+1)是多项式y=a1xm+a2xm-1+…+amx+am+1的系数；S是一个矩阵,用来估计预测误差

(2)polytool(x,y,m) 调用多项式回归GUI界面，参数意义同polyfit

2、预测和预测误差估计
(1)Y=polyval(p,x)求polyfit所得的回归多项式在x处的预测值Y

(2)[Y,DELTA]=polyconf(p,x,S,alpha)求polyfit所得的回归多项式在x处的预测值Y及预测值的显著性为1-alpha的置信区间Y±DELTA，alpha缺省时为0.5

3、实例演示说明
观测物体降落的距离s与时间t的关系，得到数据如下表，求s的表达式(即回归方程s=a+bt+ct2)

t (s) 1/30 2/30 3/30 4/30 5/30 6/30 7/30
s (cm) 11.86 15.67 20.60 26.69 33.71 41.93 51.13

t (s) 8/30 9/30 10/30 11/30 12/30 13/30 14/30
s (cm) 61.49 72.90 85.44 99.08 113.77 129.54 146.48

解法一：直接作二次多项式回归

1. >>t=1/30:1/30:14/30;
2. >>s=[11.86 15.67 20.6026.69 33.71 41.93 51.13 61.49 72.90 85.44 99.08 113.77 129.54146.48];
3. >>[p,S]=polyfit(t,s,2)
4. p =
5. 489.2946 65.8896 9.1329
6. S =
7. R: [3x3double]
8. df: 11
9. normr: 0.1157

1. >>t=1/30:1/30:14/30;
2. >>s=[11.86 15.67 20.6026.69 33.71 41.93 51.13 61.49 72.90 85.44 99.08 113.77 129.54146.48];
3. >>T=[ones(14,1) t'(t.^2)'];
4. >>[b,bint,r,rint,stats]=regress(s',T)
5. b =
6. 9.1329
7. 65.8896
8. 489.2946
9. bint =
10. 9.0614 9.2044
11. 65.2316 66.5476
12. 488.0146 490.5747
13. r =
14. -0.0129
15. -0.0302
16. -0.0148
17. 0.0732
18. 0.0040
19. 0.0474
20. -0.0165
21. -0.0078
22. -0.0363
23. -0.0222
24. 0.0046
25. -0.0059
26. -0.0237
27. 0.0411
28. rint =
29. -0.0697 0.0439
30. -0.0956 0.0352
31. -0.0876 0.0580
32. 0.0182 0.1283
33. -0.0709 0.0789
34. -0.0192 0.1139
35. -0.0894 0.0563
36. -0.0813 0.0658
37. -0.1062 0.0335
38. -0.0955 0.0511
39. -0.0704 0.0796
40. -0.0793 0.0675
41. -0.0904 0.0429
42. -0.0088 0.0910
43. stats =
44. 1.0e+007 *
45. 0.0000 1.0378 0 0.0000

1. Y=polyconf(p,t,S)；
2. plot(t,s,'k+',t,Y,'r')

1、多元二项式回归Matlab命令

rstool(x,y,'model',alpha)
输入参数说明：
x：n*m矩阵；
Y：n维列向量；
alpha：显著性水平(缺省时为0.05)；
mode：由下列4个模型中选择1个(用字符串输入,缺省时为线性模型)


2、实例演示说明
设某商品的需求量与消费者的平均收入、商品价格的统计数据如下,建立回归模型,预测平均收入为1000、价格为6时的商品需求量
需求量 100 75 80 70 50 65 90 100 110 60
收入 1000 600 1200 500 300 4001300 1100 1300 300
价格 5 7 6 6 8 7 5 4 3 9

解法一：选择纯二次模型

y=β0+β1x1+β2x2+β11x1^2+β22x2^2

1. %直接用多元二项式回归如下
2. x1=[1000 600 1200 500 300400 1300 1100 1300 300];
3. x2=[5 7 6 6 8 7 5 4 39];
4. y=[100 75 80 70 50 65 90 100110 60]';
5. x=[x1' x2'];
6. rstool(x,y,'purequadratic')

1. >>beta, rmse
2. beta =
3. 110.5313
4. 0.1464
5. -26.5709
6. -0.0001
7. 1.8475
8. rmse =
9. 4.5362

由此得回归模型为：y=110.5351+0.1464x1-26.5709x2-0.0001x1^2+1.8475x2^2
解法二：将上面的模型转换为多元线性回归

y=β0+β1x1+β2x2+β11x1^2+β22x2^2

1. >>X=[ones(10,1) x1'x2' (x1.^2)' (x2.^2)'];
2. >>[b,bint,r,rint,stats]=regress(y,X);
3. >>b,stats
4. b =
5. 110.5313
6. 0.1464
7. -26.5709
8. -0.0001
9. 1.8475
10. stats =
11. 0.9702 40.6656 0.000520.5771

爱华网本文地址 » http://www.aihuau.com/a/25101018/374389.html