爱华网题文：
已知：如图，△ABC是⊙O的内接正三角形，点D是的中点
更多阅读
已知，如图中，等边△ABC和点P，设点P到△ABC三边AB、AC、BC的距 三角形abc中ac等于bc
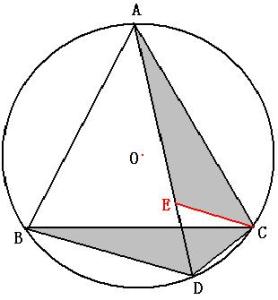
题文已知，如图中，等边△ABC和点P，设点P到△ABC三边AB、AC、BC的距离分别为h1、h2、h3，△ABC的高为h，若点P在一边BC上（如图①），此时h3=0，可得结论：h1+h2+h3=h。请直接应用上述信息解决下列问题：当点P在△ABC内（如图②）、点P在△ABC外（如图③）这两种
如图，矩形ABCD的顶点A在第一象限，AB∥x轴，AD∥y轴，且对角线的 ac是矩形abcd的对角线
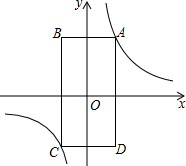
（2014·温州）如图，矩形ABCD的顶点A在第一象限，AB∥x轴，AD∥y轴，且对角线的交点与原点O重合．在边AB从小于AD到大于AD的变化过程中，若矩形ABCD的周长始终保持不变，则经过动点A的反比例函数y=kx（k≠0）中k的值的变化情况是（ ）A．一直增大B．一直减
已知a,b是单位向量,ab的向量积=0,若向量c满足|c-a-b|=1,则C的取值 同时满足两个条件取值
c-(a+b)|^2=|c|^2+|a+b|^2-2c·(a+b)=|c|^2+2-2sqrt(2)|c|cos<c,a+b>=1即：cos<c,a+b>=(|c|^2+1)/(2sqrt(2)|c|)∈[-1,1](|c|^2+1)/(2sqrt(2)|c|)≤1，可得：sqrt(2)-1≤|c|≤sqrt(2)+1(|c|^2+1)/(2sqrt(2)|c|)≥-1自动满足，不用解
三角形内周长最短的内接三角形 圆内接三角形周长
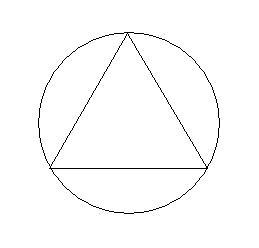
问题是这样的：证明：在△ABC的每条边上各取一点D、E、F，△DEF称为△ABC的内接三角形。试在锐角三角形ABC的所有内接三角形中，求周长最短的三角形。证明：可将此题分三步来做（1）设D是BC上固定点，求此时的周长最短的内接三角形。 作D关于A
已知宇宙有多大 宇宙外面是什么
已知宇宙有多大已知宇宙是个什么样子 ? 它究竟有多大？困扰了人们几千年。远古时期，先民们的认识很幼稚。我国古代有盖天说、渾天说和宣夜说。盖天说认为天地如同心球穹状（半球状），天和