lingo求解非线性规划 lingo求解非线性规划 用LINGO软件求解“非线性规划”问题

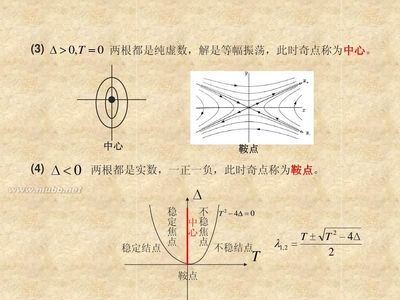
用LINGO软件求解“非线性规划”问题

丁老师(超盾博客)

一.选址问题（选取位置，使总运量最小）

例某工程，6个工地同时开工，每个工地的位置Mi(ai,bi)，距离值(单位：km)、水泥日需求量d(t)(单位：吨)由下表给出：

MiM1

1.251.253

M2

8.750.755

M3

0.54.754

M4

5.7557

M5

36.56

M6

7.257.7511

aibid(t)

目前暂定2个临时料场位于P(5,1)、Q(2,7)用于存储水泥，日储量20吨。假设从料场到工地之间均可开通直线道路相连。试寻找更好的料场位置，使得总运输量（吨·公里）更小。解将题目和表格进行整理得到：

6个工地

i(程序j)

M1

1.251.253

M2

8.750.755

M3

0.54.754

M4

5.7557

M5

36.56

M6

7.257.7511

ai(程序a(j))

工地坐标

bi(程序b(j))

需求demand假设：(1)

d(t)(程序d(j))

P(p1,p2)、Q(q1,q2)为料场；

(2)从P调c1j吨水泥到Mj，从Q调c2j吨水泥到Mj(1表示P，2表示Q)，j=1,…,6.“总吨·公里”的表示方法：“总：

∑

；吨：c；公里：两点间距”，目标函数是“非

线性”的，根据上述“总吨·公里”的表示方法得到“非线性”规划模型：

minf=c11(p1−1.25)2+(p2−1.25)2+c12(p1−8.75)2+(p2−0.75)2

+c13(p1−0.5)2+(p2−4.75)2+c14(p1−1.25.75)2+(p2−5)2+c15(p1−3)2+(p2−6.5)2+c16(p1−7.25)2+(p2−7.75)2+c21(q1−1.25)2+(q2−1.25)2+c22(q1−8.75)2+(q2−0.75)2+c23(q1−0.5)2+(q2−4.75)2+c24(q1−5.75)2+(q2−5)2+c25(q1−3)2+(q2−6.5)2+c26(q1−7.25)2+(q2−7.75)2

⎧⎪⎪cij≥0

⎪c+c=3⎫21⎪11⎪⎪c12+c22=5⎪⎪c+c=4⎪2⎪13⎪23s.t.⎨⎬⇒c1j+c2j=dj⇒∑cij=djc+c=7i=124⎪14⎪⎪c15+c25=6⎪⎪⎪⎪c16+c26=11⎪⎭⎪6⎪c11+c12+c13+c14+c15+c16≤20⎫⎬⇒∑cij≤ei⎪c+c+c+c+c+c≤20j=12223242526⎭⎩21(j=1,...,6)(i=1,2)

用LINGO9.0求解，首先分析此问题中的向量和矩阵，有：

(1)3个6维向量：a,b,d；

(2)3个2维向量：p,q,e，其中p和q表示题目中给出的最初暂定的两个料场的坐标；

(3)1个2×6调度矩阵：c.

LINGO总程序：

sets:

demand/1..6/:a,b,d;!3个6维向量;

supply/1..2/:p,q,e;!3个2维向量;

link(supply,demand):c;!1个2×6调度矩阵;

endsets

data:

a=1.25,8.75,0.5,5.75,3,7.25;

b=1.25,0.75,4.75,5,6.5,7.75;

d=3,5,4,7,6,11;

e=20,20;

enddata

init:

!迭代初始点;

p=5,2;

q=1,7;

endinit

!link(i,j):c(i,j)表示2×6调度矩阵;

![obj]表示在结果中标注目标函数所在行代码;

[obj]min=@sum(link(i,j):c(i,j)*((p(i)-a(j))^2+(q(i)-b(j))^2)^(1/2));

!先变i后变j;

@for(demand(j):[demand_con]@sum(supply(i):c(i,j))=d(j););!先变j后变i;

@for(supply(i):[supply_con]@sum(demand(j):c(i,j))<=e(i););@for(supply(i):@free(x);@free(y););!所有变量可取负值;end

点击保存后，按“Ctrl+S”运行得到结果：

Objectivevalue:85.26604(即：总运输量为85.26604吨·公里)VariableValueReducedCost

P(

P(

Q(

Q(1)2)1)2)3.2548837.2500005.6523327.7500000.0000000.8084079E-070.0000000.2675276E-06

P(1)、P(2)、Q(1)、Q(2)的值即为对初始点（题给最初临时料场）优化迭代后得到的料场的选取，即料场选取在P(p1,p2)=P(3.254883,5.652332)与Q(q1,q2)=Q(7.250000,7.750000)比较好。注意：程序中的P(1)对应数学式中的p1，但程序中的P(2)对应的是数学式中的q1而不是p2。

爱华网本文地址 » http://www.aihuau.com/a/302651/162014141259.html