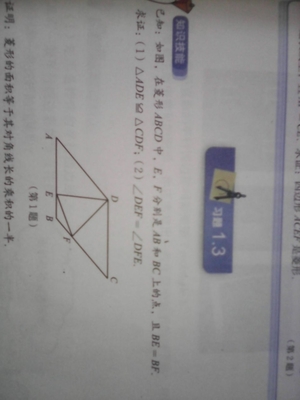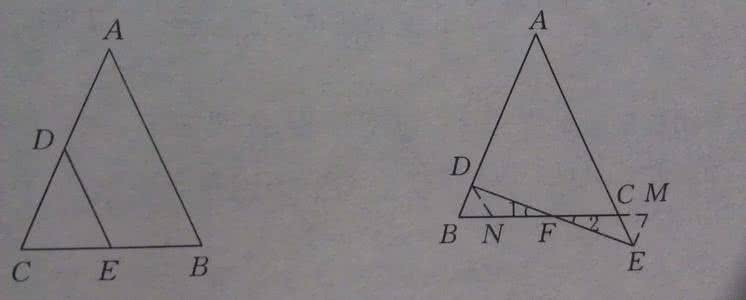
下面一道和直角三角形折叠有关的几何证明题,需要作辅助线构造相似三角形,才能顺利解决。但辅助线的作法比较灵活,通过探究此例辅助线的作法,能够训练思维的灵活性、深刻性,从而提高数学能力。下面从构造相似三角形的角度出发,探究四种辅助线的作法。例如图1,Rt△ABC中,AB=AC,点M在AC上,点N在BC上,沿MN翻折使点C恰好落在斜边AB上的点P.(1) 当P为AB中点时,求证: .(2) 当P不是AB中点时,是否仍然成立?若成立,请给出证明。析解:(1)如图1, P为AB的中点,则PA=PB,要证,所以应证CM=CN.连结CP,由PA=PB,CA=CB,得CP⊥AB.可知△CMN与△PMN完全重合, 得CM=PM,CN=PN.∴MN⊥CP.(MN是PC的垂直平分线)∴MN∥AB.∴==1.∵,∴.(2) 如图2, 此时仍然成立.如何证明关键是怎么作辅助线,将成比例线段的四条线段集中在一块,利用全等三角形和相似三角形的知识来研究。辅助线一由,考虑从线段AB 的内分点P作AC的平行线,构造出相似三角形,再从已知分析寻找证明思路。证:如图(2),作PQ//AC,则PQ⊥BC,连结PC.∵PQ∥AC,∴.而PQ=QB,∴.(如果以作为中间比,须证。于是从思考△PQC∽△NCM是否成立。)由已知可得PC⊥MN,MC⊥CN,∴∠CMN=∠PCQ,∴Rt△PCQ∽Rt△NMC.∴.∴.辅助线二仍然考虑从P出发构造相似三角形和全等三角形。证:如图3. 作PH⊥AB于P交AC于H,作AQ∥BC,于PN的延长线交于Q,可得△PAQ∽△PBN,有.∵PH⊥AB于P,∠PAH=45°,∴PA=PH,∠PHM=∠PAQ=45°,∵△CMN≌△PMN,∠MPN=Rt∠.∠1+∠3=∠2+∠3=Rt∠∴∠1=∠2, ∴△PHM≌△PAQ(ASA) ,∴PQ=PM.∴.辅助线三由可知,PA、PM在△PAM中,而PB、PN在△PBN中,显然不易证这两三角形相似,于是想办法作辅助线构造一个与△PAM相似的三角形。证:作PQ=PN交BC于Q,如图4. ∠PNQ=∠PQN,∠PNC与∠PMC互补,∠PMA与∠PMC互补,∠PMA=∠PQB,又∠A=∠B=45°,∴△PMA∽△PQB, ∴.又PQ=PN∴成立。而PM=PN,PN=CN,∴.辅助线四根据以上三种辅助线的作法,不难想到第四种作法。证:如图5,作PH⊥AC于H,PG⊥BC于G ,易证Rt△AHP∽Rt△BGP, 则,再证Rt△AHP∽Rt△PGN,∴问题可以得到解决。最科学、最实用、最接地气的中高考数学知识分享,专为中高考考生提供丰富的备考技巧、复习资料、精品课程等,致力帮助初三和高三学生迎战中高考。欢迎关注微信公众号:zgkcc100
 爱华网
爱华网