一. 构造平行四边形证两线段平行
例1. 已知如图,平行四边形ABCD的对角线AC和BD交于O,E、F分别为OB、OD的中点,过O任作一直线分别交AB、CD于G、H。
求证:GF//EH。
证明:连结GE、FH
四边形ABCD是平行四边形
又
四边形EHFG是平行四边形
二. 构造平行四边形证两线段相等
例2. 如图,中,D在AB上,E在AC的延长线上,BD=CE连结DE,交BC于F,∠BAC外角的平分线交BC的延长线于G,且AG//DE。
求证:BF=CF
分析:过点C作CM//AB交DE于点M,可以证明BD=CM,然后再利用平行四边形的性质得到BF=CF
证明:过点C作CM//AB交BE于点M,连接BM、CD,则∠CME=∠ADE
四边形BMCD为平行四边形
故BF=CF
三. 构造平行四边形证线段的不等关系
例3. 如图,AD是的边BC上的中线,求证:
分析:欲证,即要证,设法将2AD、AB、AC归结到一个三角形中,利用三角形任意两边之和大于第三边来证明。注意到AD为的中线,故可考虑延长AD到E,使DE=AD,则四边形ABEC为平行四边形。从而问题得证。
证明:延长AD到E,使DE=AD,连结BE、EC
摘要:四边形ABEC是平行四边形 在 中,AEAB+BE 即2ADAB+AC 点评:此题是利用三角形三边关
四边形ABEC是平行四边形
在中,AE<AB+BE
即2AD<AB+AC
点评:此题是利用三角形三边关系定理、平行四边形的判定,通过延长中线将证明三角形中三条线段间的不等关系,转化为三角形三边之间的关系,从而使问题迎刃而解。
四. 构造平行四边形证线段的倍分关系
例4. 如图,分别以中的AB、AC为边向外作正方形ABEF和正方形ACGH,M是BC的中点,求证:FH=2AM
证明:延长AM到D,使MD=AM,连结BD、CD,
是BC的中点
四边形ABDC为平行四边形
又AF=BA,AH=AC=BD
故FH=2AM
五. 构造平行四边形证两线段互相平分
例5. 平面上三个等边三角形两两共有一个顶点,如图所示,求证:CD与EF互相平分
分析:要证CD与EF互相平分,须证四边形DFCE是平行四边形
证明:连结DE、DF、AF易知AD=AB=BD
又AE=AC,AD=AB
∠DAE=60°-∠EAB=∠BAC
四边形DECF是平行四边形
故CD与EF互相平分
六. 构造平行四边形证角的不等关系
例6. 如图,在梯形ABCD中,AD//BC,对角线AC>BD摘要:求证:DBCACB 证明:过点D作DE//AC交BC的延长线于点E,则四边形ACED是平行四边形 又
求证:∠DBC>∠ACB
证明:过点D作DE//AC交BC的延长线于点E,则四边形ACED是平行四边形
又
在中,∠DBE>∠E
七. 构造平行四边形证线段的和差关系
例7. 如图,中,点E、F在边AB上,AE=BF,ED//AC//FG,求证:ED+FG=AC
证明:过E作EH//BC交AC于H
四边形CHED为平行四边形
又AE=BF,
同步练习:
1. 如图1,在梯形BCED中,DE//BC延长BD、CE交于A,在BD上截取BF=AD。过F作FG//BC交EC于G,求证:DE+FG=BC。
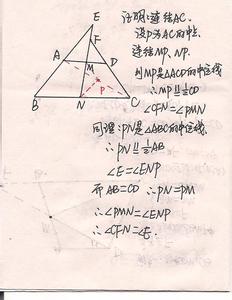
2. 如图2,中,AB=AC,E是AB上一点,F是AC延长线上一点,BE=CF,EF交BC于D。
求证:DE=DF
3. 如图3,平行四边形ABCD中,E、G、F、H分别是四条边上的点,且AE=CF,BG=DH,求证:EF与GH互相平分
4. 如图4,已知AB=AC,B是AD的中点,E是AB的中点,求证CD=2CE
5. 已知:如图5在四边形ABCD中,AB=DC,AD=BC,点E在BC上,点F在AD上,AF=CE,EF与对角线BD相交于点O,求证:O是BD的中点。
提示:
1. 过点F作FM//AC交BC于点M,则有平行四边形FMCG。
2. 过E作EG//AC交BC于G,连结CE、GF。摘要:3. 连结FH、HE、EG、GF 4. 延长CE至F,使EF=CE,连结AF、BF。 5. 连结BF
3. 连结FH、HE、EG、GF
4. 延长CE至F,使EF=CE,连结AF、BF。
5. 连结BF、DE
四边形ABCD是平行四边形
又
四边形BEDF是平行四边形
O是BD的中点

 爱华网
爱华网