white检验步骤 white检验步骤 White检验

一、 White检验

❶、用OLS法估计，并求出e2、x2序列。 ❷、回归e2 c x x2得：

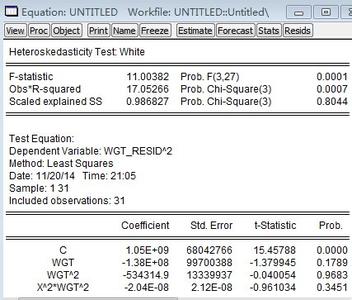
Dependent Variable: E^2 Method: Least Squares Date: 11/11/11 Time: 21:06 Sample: 1 21

Included observations: 21

C X X2

R-squared Adjusted R-squared S.E. of regression Sum squared resid Log likelihood F-statistic Prob(F-statistic)

Coefficient 823375.5 -3605.578 4.742387

Std. Error 130273.4 553.5894 0.532352

t-Statistic 6.320365 -6.513091 8.908366

Prob. 0.0000 0.0000 0.0000 351198.3 454261.0 27.15649 27.30571 27.18888 2.015035

0.860705 Mean dependent var 0.845228 S.D. dependent var 178711.1 Akaike info criterion 5.75E+11 Schwarz criterion -282.1432 Hannan-Quinn criter. 55.61118 Durbin-Watson stat 0.000000

X和X2的t检验值很显著。

❸、计算统计量n*R2，n*R2=21*0.860705=18.074805。由white检验知，在ａ=0.05，查X2分布表得X20.05(2)=5.9915，n*R2=18.074805>X20.05(2)=5.9915,所以拒绝原假设，表明模型存在异方差

二、 ARCH检验

❶、提出假设：

H0：ａ1=ａ2=ａ3，H1:ａj(j=1，2)中至少有一个不为0。

❷、回归原模型，求出残差e，并计算出残差平方序e2t-1、e2t-2,并回归e2 c e2(-1) e2(-2)得

Dependent Variable: E2 Method: Least Squares Date: 11/11/11 Time: 22:09 Sample (adjusted): 3 21 Included observations: 19 after adjustments Coefficient Std. Error t-Statistic Prob.

C 204070.3 100029.5 2.040101 0.0582

E2(-1) -0.078393 0.223052 -0.351457 0.7298 E2(-2) 0.267413 0.118184 2.262681 0.0379 R-squared 0.279746 Mean dependent var 279134.7 Adjusted R-squared 0.189714 S.D. dependent var 251501.6 S.E. of regression 226391.4 Akaike info criterion 27.64186 Sum squared resid 8.20E+11 Schwarz criterion 27.79098 Log likelihood -259.5976 Hannan-Quinn criter. 27.66710 F-statistic 3.107188 Durbin-Watson stat 2.119843 Prob(F-statistic) 0.072425 ❸、在H0成立的条件下，（n-p）*R渐进服从X2（p）。（n-p）*R2=17*0.279746=4.755682>X20.1(2)=4.60517。拒绝原假设，说明存在异方差。

爱华网本文地址 » http://www.aihuau.com/a/306751/139764499089.html