博弈论案例分析
——“占座大战”博弈
班级:
姓名:
学号:
博弈论(Game Theory),亦名“对策论”、“游戏理论”,属应用数学的一个分支, 博弈论已经成为经济学的标准分析工具之一。目前在生物学、经济学、国际关系、计算机科学、政治学、军事战略和其他很多学科都有广泛的应用。博弈论主要研究公式化了的激励结构间的相互作用。是研究具有斗争或竞争性质现象的数学理论和方法。也是运筹学的一个重要学科。 博弈论考虑游戏中的个体的预测行为和实际行为,并研究它们的优化策略。生物学家使用博弈理论来理解和预测进化论的某些结果。
.博弈论是指某个个人或是组织,面对一定的环境条件,在一定的规则约束下,依靠所掌握的信息,从各自选择的行为或是策略进行选择并加以实施,并从各自取得相应结果或收益的过程,在经济学上博奕论是个非常重要的理论概念。
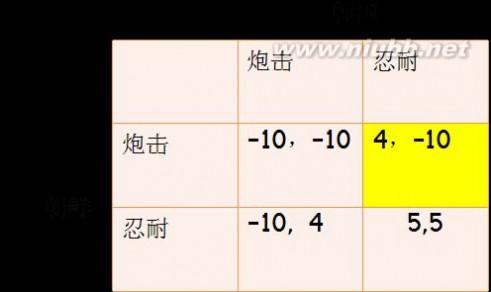
什么是博弈论?古语有云,世事如棋。生活中每个人如同棋手,其每一个行为如同在一张看不见的棋盘上布一个子,精明慎重的棋手们相互揣摩、相互牵制,人人争赢,下出诸多精彩纷呈、变化多端的棋局。博弈论是研究棋手们 “出棋” 招数中理性化、逻辑化的部分,并将其系统化为一门科学。换句话说,就是研究个体如何在错综复杂的相互影响中得出最合理的策略。
现在,我们就讨论一下生活中的博弈;
大学生活中,生活也是比较的丰富,其中,吃饭也是很重要的部分,大家一般都是在学校食堂吃饭,由于大家吃饭的时间比较集中,所以吃饭的时候人数特别多,食堂座位有限,同学们也希望在食堂买完饭后不用再找座位,因此很多同学在买饭之前就用自己的私人物品占座位,为此,食堂也经常发生因为占座位而引起的纠纷。在这里称为“占座大战”博弈,就这个博弈问题进行讨论;
现在就这个问题来进行一个博弈论的分析,两个发生纠纷的人都有两个选择,分别是U(冲上去进行理论,争取座位),D(选择退让,找其他的座位),若两人都进行理论,争取座位的话,很有可能就是两败俱伤,两个人也可能因意见不合而进而出现打架的现象,而且在食堂这个公共场所,对大家的形象都有着很不好的影响;如果一方选择退让,而另外一方则选择理论,则结果可能就是一方另找座位,有些损失,一方占领了座位,取得了胜利;还有就是双方都选择了退让,将座位让给其他人;
根据以上的分析,现在有如下的支付图:
参与人2
U
D
U -2,-2 1,-1
参与人1
D -1,1 0,0
求解过程(箭头法):
参与人2
U
参与人1
D
现在求解这个博弈问题:由博弈问题的Nash均衡可以知道,在以上的博弈问题中存在着两个纯战略Nash均衡——(U,D)和(D,U),就是说,在整个的博弈中,两个人中有一个人退让,寻找其他的座位,另外一个人进行争论得到座位。
对于这个结果,我们可以这样认识:我们现在认为两个人都是理性的,在一个参与人预测到另一方将会进行理论时,明智的选择就是退让,避免更大的损失,而当预测到对方将会选择退让时,则进行理论,以求得最大的胜利;可以将Nash均衡作为此次“抢座大战”的一致性预测,而其它的结果(U,U)和(D,D)都将不会是一致性预测,就(U,U)来说,对双方而言都不是最好的结果,且受到的损失也会是最大的;再就是(D,D),双方都进行退让,也是不太可能的,当有一方有退让的迹象,另外一方就可能进行理论来求得利益的最大,因此这个结果也不会是一致性的预测,不会是一个均衡,必然会偏离的,向着Nash均衡的方向偏移。
在上面的这个博弈中,出现了两个Nash均衡,在一个博弈问题中,如果只存在一个Nash均衡,那么Nash均衡作为一致性的预测,应该说是很有效的。但是,如果像这个“座位大战”博弈一样,存在两个Nash均衡,那么Nash均衡作为博弈解的意义也就相对弱化了。我们不能进行预测,到底是谁进行了退让,是谁进行了进一步的理论,得到座位;如果两个人对两个均衡到底哪一个会出现的预测不一致就会出现问题,比如说,参与人1预测博弈的解为自己理论,对方退让,而参与人2预测的是对方退让,自己理论,那么最后出现的真正的结果将不会是Nash均衡(U,D),也不会是(D,U),而会是损伤最大的非Nash均衡(U,U)。
由以上的分析,出现了nash均衡的多重性,我们暂且用Schellling的“焦点效应”来解决,将均衡聚焦到一个上,我们分以下情况:
(1),两个参与者之间,有一个是女生,一个是男生,则很有可能是博弈的解偏向女生的一边,男生让着女生;
(2),两个参与者之间,有一个是年轻人,一个是相对年老的人(或者小孩,残疾人等弱势群体),则很有可能是博弈的解偏向年老(或者小孩,残疾人等弱势群体)的一边,年轻人让给年老者(或者小孩,残疾人等弱势群体);
(3),两个参与人都遵守食堂的规则,由食堂的管理人员来处理,按照食堂的规则,把座位给先到的人;
(4),两个参与人中,一个是争强好胜之人,一个则习惯忍气吞声,不愿惹是生非,则博弈的结果很有可能会偏向争强好胜之人;
(5),进行一些磋商,如:参与人中有一个赶时间,需要马上吃完饭去办事,而另外一个则时间充裕,进行一番协商之后。则博弈的结果很有可能是偏向时间紧急的人,让他得到座位;
等等一些其他的情况,也可以使博弈的解偏向一方;
跟这个博弈相似的一个经典案例就是我们学过的一个“斗鸡博弈”,两只公鸡面对面争斗,继续斗下去,两败俱伤,一方退却便意味着认输。在这样的博弈中,要想取胜,就要在气势上压倒对方,至少要显示出破釜沉舟、背水一战的决心来,以迫使对方退却。但到最后的关键时刻,必有一方要退下来,除非真正抱定鱼死网破的决心。
这类博弈不胜枚举。如两人反向过同一独木桥,一般来说,必有一人选择后退。在该种博弈中,非理性、非理智的形象塑造往往是一种可选择的策略运用。如那种看上去不把自己的生命当回事的人,或者看上去有点醉醺醺、傻乎乎的人,往往能逼退独木桥上的另一人。
还有夫妻争吵也常常是一个“斗鸡博弈”,吵到最后,一般地,总有一方对于对方的唠叨、责骂装聋作哑,或者干脆妻子回娘家去冷却怒火。冷战期间,美苏两大军事集团的争斗也是一种“斗鸡博弈”。在企业经营方面,在市场容量有限的条件下,一家企业投资了某一项目,另一家企业便会放弃对该项目的觊觎。
看出这类博弈的应用也还还是很广泛的。人们常提到的“上有政策、下有对策”,其实是对管理者与被管理者之间的动态博弈的一种描述,面对上边的政策,下边寻求对策是正常的、必然的。从“博弈论”的角度讲,上边的政策制定必须在考虑到下边可能会有的对策的基础上进行,否则,政策就不会是科学、合理的。
其实我们身边充满了博弈,或者说,我们身边的许多行为、现象都可用博弈来概括。“博弈论”不仅属于经济学,也理应属于社会学、政治学、心理学、历史学等,这些学科也有理由分享“博弈论”那旖旎的学术风光和精细的分析技巧。
 爱华网
爱华网