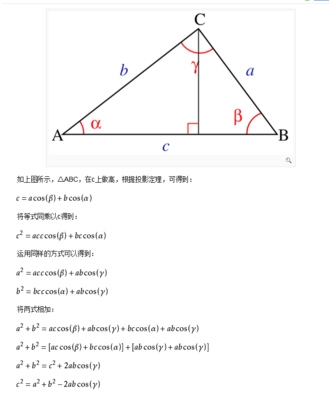
已知:在如图1所示的锐角三角形ABC中,CH⊥AB于点H,点B关于直线CH的对称点为D,AC边上一点E满足∠EDA=∠A,直线DE交直线CH于点F.
(1) 求证:BF∥AC;
(2) 若AC边的中点为M,求证:;
(3) 当AB=BC时(如图2),在未添加辅助线和其它字母的条件下,找出图2中所有与BE相等的线段,并证明你的结论.
图1 图2
试题答案
证明:(1)如图6. ∵ 点B关于直线CH的对称点为D, CH⊥AB于点H, 直线DE交直线CH于点F, ∴ BF=DF,DH=BH. ∴ ∠1=∠2. 又∵ ∠EDA=∠A,∠EDA=∠1, ∴ ∠A=∠2. ∴ BF∥AC. (2)取FD的中点N,连结HM、HN. ∵ H是BD的中点,N是FD的中点, ∴ HN∥BF. 由(1)得BF∥AC, ∴ HN∥AC,即HN∥EM. ∵ 在Rt△ACH中,∠AHC=90°, AC边的中点为M, ∴ . ∴ ∠A=∠3. ∴ ∠EDA=∠3. ∴ NE∥HM. ∴ 四边形ENHM是平行四边形∴ HN=EM. ∵ 在Rt△DFH中,∠DHF=90°,DF的中点为N, ∴ ,即. ∴ . ………………………………………………………… 4分 (3)当AB=BC时,在未添加辅助线和其它字母的条件下,原题图2中所有与BE相等的线段是EF和CE. (只猜想结论不给分) 证明:连结CD.(如图8) ∵ 点B关于直线CH的对称点为D,CH⊥AB于点H, ∴ BC=CD,∠ABC=∠5. ∵ AB=BC, ∴ , AB=CD.① ∵ ∠EDA=∠A, ∴ ,AE=DE.② ∴ ∠ABC=∠6=∠5. ∵ ∠BDE是△ADE的外角, ∴ . ∵ , ∴ ∠A=∠4.③ 由①,②,③得 △ABE≌△DCE.………………………………………5分 ∴ BE= CE. ……………………………………………………………… 6分 由(1)中BF=DF得 ∠CFE=∠BFC. 由(1)中所得BF∥AC 可得 ∠BFC=∠ECF. ∴ ∠CFE=∠ECF. ∴ EF=CE. ∴ BE=EF. ……………………………………………………………… 7分 ∴ BE=EF=CE. (阅卷说明:在第3问中,若仅证出BE=EF或BE=CE只得2分)
 爱华网
爱华网