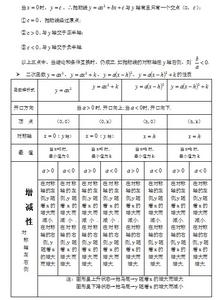
(1)求n的取值范围
(2)若n>1/36,且AO + BO = 3CO,求抛物线的解析式以及点A,B,C的坐标
(3)在(2)的情形下,点P,Q分别从A,O两点出发,沿AB,OC方向运动,Q点运动的速度是P点运动速度的2倍,当P点运动到B点时,P,Q两点停止运动,设AP=k,问是否存在这样的K 值,使一P,Q,O为顶点的三角形与三角形AOC相似?若存在,求出所有这样的k值,若不存在,请说明理由。 这是中考类型的综合题。讲解一下的目的是:学生做得太慢了,临场可能浪费时间,我系统地讲一遍。 分析与解答:首先在脑子里建立一个大致的图像,如下: 令y=0, x2/8+6n x +72 n2-2 n =0 (1) 首先应该考虑⊿>0。∵抛物线与x轴交于两点, ∴ ? = (6n)2 - 4×(1/8)×(72n2-2n) = n
得n的取值范围: n > 0 (2) ∵n>1/36, 令x=0, 则有:C =72n2-2n =2n(36n - 1) > 0, ∴ C在y轴上方
这个地方有一个关键点:判断交点的位置。 显然用韦达定理比“先求出根的值”再讨论或判断正负,要简洁。 由x2/8+6n x +72 n2-2 n =0 ∵x1+x2<0, x1·x2 >0 ∴x1、x2均为负值。(看图二)
又:OA + OB=3OC,即|-x? |+|x?|=72n2-2n
解得:n= 1/4 有 A(-8, 0), B(-4, 0), C(0, 4) y = x2/8+ 3x/2 + 4 (3)这一问没有什么了, 但是我习惯上来先回答 这样的点存在,且有两个。(希望学生注意) ∵OA = 8, OC = 4, (注意:OA =2OC) 使一P,Q,O为顶点的三角形与三角形AOC相似, ∴满足OP = 2OQ或OQ = 2OP (有两解)
先用坐标表示:AP = K (0< K ≤ 4 = AB), OQ = 2K
P(-8+K, 0), Q(0, 2K), OP =8 – K,
1° OP = 2OQ K = 8/5
2° OQ = 2OP , 2K = 2(8-K)
K = 4 (此时P与B重合)
P(-4, 0), Q(0, 8)。
总之,中考最后一题基本上没有什么难度,只要在仔细的条件下,追求一点速度就可以了。

 爱华网
爱华网