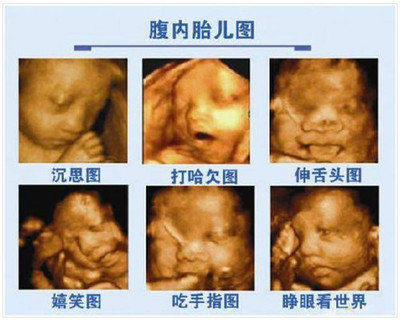
熟悉神秘学的都认识左图是一个梅尔卡巴,又叫六芒星,是形成宇宙的基本结构之一。它由两个相交的正三角形构成,有六个顶点并且内接于一个圆形。但实际上那只是梅尔卡巴在二维平面的投影,梅尔卡巴本身是多维的,在每个维度的空间都有不同的展现。右图就是三维空间的梅尔卡巴,是由两个正四面体相交得到的“星形四面体”结构,有八个顶点并且内接于一个球体。由此我们可以联想,四维空间的梅尔卡巴是由两个相交的超四面体形成的“超星体”结构,有十个顶点并且内接于一个四维超球体之中。可见,某些神秘学几何图形如犹太教的卡巴拉、古印度教的梅尔卡巴、苏菲秘教九宫图、佛教曼陀罗、道家阴阳太极图等其实都是在二维平面上的简化版,真正的结构和意义要复杂得多。
6.莫比乌斯环、克菜因瓶及宇宙的边界
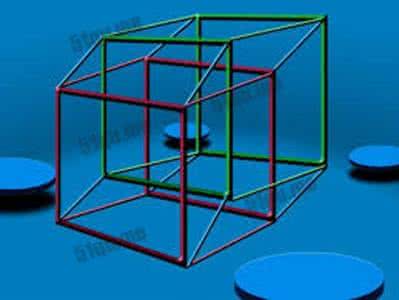
一个纸条有正面和反面,如果不充许从边界绕过去,有没有办法从一面到另一面呢?有,就是把这个纸条的一端扭转180度再和另一端连接起来,形成一个莫比乌斯环(如上面左图)。实际上,这个扭曲的二维结构是没有正反面之分的,仔
细观察就会发现,只要你在这个纸面上沿着一个方向走,就能够经过这个纸条的所有位置并且回到原点。然而,莫比乌斯环表面虽然是一个二维结构,但是它本身却只能在三维空间存在。
那么三维空间有没有对应的结构呢?有,就是克菜因瓶(如右图)。在这个奇怪的管状物里行走,你能经历所有空间的正面和反面。其实这只是一种简化的表示,真正的克菜因瓶是不可能在三维空间里画出来的,因为它本身存在于四维空间。克菜因瓶好像有一个与自己相交的部分,然而在四维空间它并不相交,就像莫比乌斯环在三维空间不相交一样。
事实上,我们的宇宙就是一个由扭曲的空间形成的克菜因瓶结构。这个宇宙的大小是有限的,但是并没有边界,你沿着同一个方向走会经过该直线上所有空间的正面和反面并且回到起点。
7.超球面、内层空间与卡萨拉行星门
既然这个宇宙是有限且没有边界的,那么从一个位置到另一个位置是不是只能靠漫长的太空旅行呢?当然不是。前面已经论述过,宇宙本身是多维的,而“低维空间不过是高维空间的表皮”。因此,虽然我们这个三维空间看起来很充实,但实际上只是四维空间“超球面”的一部分,黑洞就是穿越球表面的洞。在这个超球体内部还有空间,是三维世界永远无法到达的,称为“内层空间”。内层空间有很多小的“入口”和“接线”,类似于虫洞从表面的一个位置连接到另一个位置,或者从一个维度连接到另一个维度,这些就是GA所说的卡萨拉行星门,也是UFO穿越时空的主要方法之一。
 爱华网
爱华网