中学数学:认真梳理知识点,三角形全等问题不再难
学好数学的关键就在于要适时适量地进行总结归类,认真梳理知识点,三角形全等问题不再难。
1、全等三角形:能够完全重合的两个三角形,叫做全等三角形.
对应边:能重合的边叫对应边。
对应角:能重合的角叫对应角。
2、全等三角形表示法:
①用符号写出一个三角形的名称
②写出全等符号 ≌
③再用符号写出另一个三角形的名称
④如≌△ABC≌△DEF 只有一种对应方式。(A→D ,B→E, C→F)
⑤注意:对应顶点的字母一定要对应。
说明; △ABC全等于△DEF (A点有三种对应方式,A →D,A→E,A→F)
3、全等变换形式:
①平移型:
②翻折型:
③旋转型:
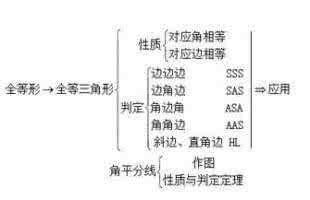
4、全等三角形有如下性质:
(1)全等三角形的对应边相等;
(2)全等三角形的对应角相等;
(3)全等三角形的对应中线、对应角平分线、对应高相等;
(4)全等三角形的面积相等,周长相等.
5、判定两个三角形全等的依据:
(1) 边边边公理(SSS):三条边对应相等的两个三角形全等
(2) 边角边公理(SAS):两边及其夹角对应相等的两个三角形全等;
(3) 角边角公理(ASA):两角及其夹边对应相等的两个三角形全等;
(4) 角边角公理的推论(AAS):两角和其中一角的对边对应相等的两个三角形全等;
(5)斜边、直角边公理(HL):斜边和一直角边对应相等的两个三角形全等.
6、全等三角形对应边对应角找法:
①、对应角所对的边是对应边;对应边所对的角是对应角。
②、公共边是对应边;公共角(对顶角)是对应角。
③、相等的边是对应边;相等的是对应角。
④、最大(小)边与最大(小)边是对应边;最大(小)角与最大(小)角是对应角。
⑤、对应角所夹的边是对应边;对应边所夹的角是对应角。
7、角平分线性质定理:角平分线上的点到这个角两边的距离相等。
角平分线判定定理: 角的内部到角两边的距离相等的点在这个角的平分线上。
8、证明两个三角形全等,必须根据已知条件与结论,认真分析图形,准确无误的确定对应边及对应角;去分析已具有的条件和还缺少的条件,并会将其他一些条件转化为所需的条件,从而使问题得到解决。
运用定理证明三角形全等时要注意以下几点。
(1)、判定两个三角形全等的定理中,必须具备三个条件,且至少要有一组边对应相等,因此在寻找全等的条件时,总是先寻找边相等的可能性。
(2)、要善于发现和利用隐含的等量元素,如公共角、公共边、对顶角等。
(3)、要善于灵活选择适当的方法判定两个三角形全等。
a、已知条件中有两角对应相等,可找:
①夹边相等(ASA)
②任一组等角的对边相等(AAS)
b、已知条件中有两边对应相等,可找
①夹角相等(SAS)
②第三组边也相等(SSS)
c、已知条件中有一边一角对应相等,可找
①任一组角相等(AAS 或ASA)②夹等角的另一组边相等(SAS)
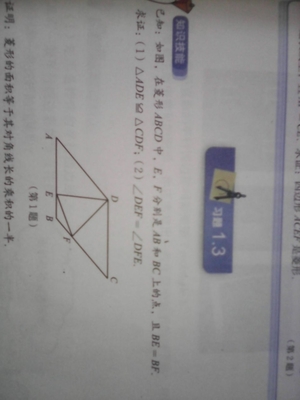
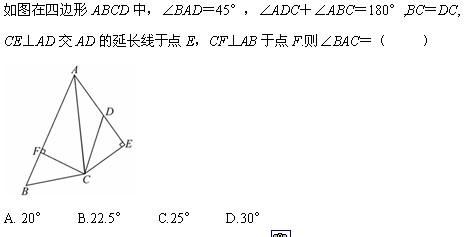
9、典例赏析
点评:通过间接条件得到直接条件,是解决问题时经常遇到的,目的是考查对知识的综合运用。
你会做吗?
点评:本题主要应用了全等三角形的有关知识和角平分线性质,解决本题的关键是把要证明相等的两条线段看作一个平分线上的点到该角两边的距离。
 爱华网
爱华网