写在前面的话:
前几天有家长看了《高考志愿填报那些事儿》,说里面怎么有安徽的案例,其实在序里已说明,为了使本书中的理论更具可读性,适当穿插个别具体或者模拟的案例,所以就用了安徽省内的案例,并不特指安徽省。用在其他省份也是好使的,其他省份家长已有反馈:风趣幽默、通俗易懂、观点明确、推理严谨。好在可以在网上更新一些东西,与书中内容互补也是很好的。
书中涉及很多高考志愿难理解的名词,我用故事的形式加以解释,本文我先把其中的一个小小的点“拎”出来详细解读一下,从另一个侧面思考我们熟悉的高考,希望可以给家长和考生一些启发。
数字看高考:
高考作为一种选拔人才的方式,是我国第一大考,没有之一。其影响力可见一斑,所以用实实在在的分数考出来的成绩公信力很高。但是目前绝大多数省份都是自主命题,这样的结果自然会有不同高低的分数线(试卷难度不同,回头另一篇单说“分数线”),这是很正常的。不过我们可以想一下,高考是什么?是一种手段,是一种方法,是一种把考生进行区分的方法。这就说到了高考试卷,一份好的高考试卷是难度适中、区分度强,适用于每名考生。无他!
以北京市为例,2014年有6万余名考生参加高考。填报志愿之前,大本上会发布一张高考成绩分布统计表,该表格是考生当年高考成绩分布情况,即不同分数段内考生数的统计表。这种表格很多省的考试院都会直接做出来,不同的是分档的精细程度不同而已。比如,北京市是10分档的统计表,江苏省为5分档的统计表,安徽省为1分档的统计表。这样通过这张表可以判断出分数段内累计的考生人数,我们可以称之为“考生密度”,不同分数段位置的考生密度不同,基本上一本线附近的考生密度最大。通过查分档表可得,北京市理科考生密度最大处为180余人/分(180人考到同一个分数),安徽省理科考生密度最大处为1200余人左右/分,河南省理科考生密度最大处为1600人左右/分。该密度与招生人数再次对比,就代表考生竞争激烈的程度。
大家之所以羡慕北京考生,是因为考生竞争小很多。
下图选取部分理科分档表做分析,想进一步分析的家长可在网上自行下载。
2014年北京市高考成绩分布表
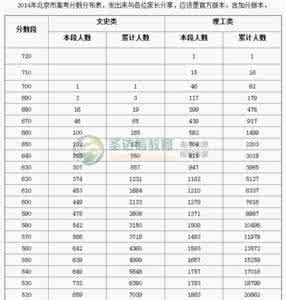
2013年北京市理科高考成绩分布(部分)
2013年北京市理科高考成绩分布(部分)
2012年北京市理科高考成绩分布(部分)
2012年北京市理科高考成绩分布(部分)
下文对2014年、2013年、2012年三年的高考成绩分布表进行分析(2013年的数据比较多一点)。从图表中我们可以看出,每10分段考生的累计人数,以及总的累积人数,这都很好理解。我们可以设想一下,如果把每名考生看作一个带有唯一“标记点”,那么这些点在一张白纸上会是一个什么样的分布呢?即每个分数段有多少人考到这个分数,把高考成绩分布表换一种表达,我们把2014年、2013年、2012年三年是数据做同样的处理,会是什么样子呢?
高考成绩分布图:
通过对比分析之后,我们发现很多有意思的东西。2014年北京市考生高考成绩分布图是一个正态分布的曲线,2013年和2012年也都是正态分布曲线。正态分布的概念很好理解,人的智力跟人的身高和商品批次质量一样,都是符合正态分布的。正态分布是本文的主题,正态分布也叫高斯分布,是正常分布,也是自然分布。这个分布本来就是存在的,只是这次全市大考(有多大?全市统一用一张试卷)把它呈现出来而已。而且我相信它也是稳定存在的,不会因为试卷的难度而发生变化,甚至与试卷无关。试卷难度仅仅是让该曲线向不同的方向移动而已,试卷变难曲线整体向靠近总分方向移动,试卷变易曲线整体向远离总分方向移动,而曲线本身并没有发生变化。我相信小到一个班级、一所学校,大到考生更多的省份、全国的考生。这些“标记点”组成的分布也是正态分布,不同的是各自曲线显示的“紧凑”程度不同,具体是什么样子的还要看数据显示成什么样子。
下图为近三年北京市理科高考成绩分布图(一分一档表):
下图为2012-2014年北京市高考理科分数线的统计,分数线划分与招生计划、录取比例等等直接相关,目前大家可以与上图做一些简单对比。
该曲线的方法很简单,就是把上文的分布表(一分一档表)换一种表达方法,把表格用曲线的方法进行表达,这样做的好处就是可以很直观地看出不同曲线之间的相关性(相关性很重要)。通过上面三条曲线对比,理科曲线最高处超过150人,文科曲线最高处超过150人,该位置的考生密度最大。三条曲线为近似的正态分布,而且他们极为相似。
文科高考成绩分布图也是正态分布,这是在意料之中的。
至于最后的一本二本怎么区分,那是招生计划的事情,不在本文讨论之列。
有点儿启示:
具体是一分档五分档还是十分档的分布表多没有关系,都可以得到同样的正态分布曲线,只是精细程度不同而已。但是我们可以得出一个结论:高考与试卷无关。那么给我们的启示是什么?这就是我们平时考试的时候,不能患得患失地盯着分数,我们要做的是掌握知识点;不要计较一城一地的得失,我们的目标是高考,每次考试都是练习。同样,到了高考那一天,我们更不应该紧张和忧虑,你要做的就是像无数次练习的那样把题目做好就行了。如果你真心付出了时间和精力,高考是不会骗人的。作为一个学长,给大家一个忠告:高考仅仅是一场考试,所有的胜负早已存在那条曲线里,你无需紧张更不要做出傻事,保持一个平常心老老实实把题目做好即可。
高考考什么?考的是你的平时成绩,是你做过的题目,更是你花在学习上的时间,时间是不会骗人的。
那么问题来了,既然高考与试卷无关,那你还紧张什么!那就抛弃所有的顾虑与情绪,静静准备那场终究要面对的战斗!
 爱华网
爱华网