网络出版时间:2014-10-29 10:55
网络出版地址:http://www.cnki.net/kcms/detail/51.1196.TP.20141029.1055.101.html
优先出版
计 算 机 应 用 研 究
第32卷
一种基于复杂网络的网络安全态势预测机制
李方伟,邓 武,朱 江
(重庆邮电大学 移动通信技术重庆市重点实验室,重庆 400065)
摘 要:针对现有态势预测方法大都是对态势值的预测,并未揭示网络态势要素动力学特征的问题,提出了一种基于复杂网络的网络安全态势预测机制,可方便而又直观的追溯安全态势中数值波动的动力学特征。其次在该机制中提出基于复杂网络的马尔科夫预测方法,实现对安全状态的有效预测。通过仿真实验分析,该机制在一定程度上能突出系统的本质行为,且能较准确的预测未来的安全状态。
关键词:网络安全;态势预测;复杂网络;马尔科夫模型;动力学特征 中图分类号:TN918.91 文献标志码:A
*
400065, China)
Abstract: the security situation. In addition, in order to predict Markov prediction method based on complex network. Through simulation condition of the system in a certain
Key Words:
安全问题,网络态势感知[1]CSA)在此背景下应运而生。
[2]、智能预测、组合预测[3]等。文献[4][5]针对态势值具有非线性特点,建立了基于神经网络的态势预测方法;文献[6]采用支持向量机预测方法解决了神经网络预测中所面临的过拟合缺陷等问题。现有方法都是预测未来网络安全态势值,并未说明态势值的大小具体代表网络所处的安全等级,不利于网络管理员采取应对措施。同时很少分析态势变化的趋势和揭示网络态势要素的动力学特征。
考虑到这些问题,本文提出了一种基于复杂网络的网络安全态势预测机制。该机制首先采用层次化的评估模型获取网络安全态势值,利用粗粒化方法把态势时间序列映射为符号序列,构建有向加权的态势复杂网络。对建立的复杂网络模型的统计
--------------------------------
基金项目:国家自然科学基金项目(61271260)
作者简介:李方伟(1960-),男,重庆人,教授,博士,主要研究方向为移动通信技术与理论、信息安全技术(lifw@cqupt.edu.cn);邓武(1987-),男,四川南充人,硕士研究生,主要研究方向为移动通信安全;朱江(1977-),男,湖北荆州人,副教授,博士,主要研究方向为认知无线电技术.
复杂网络的角度揭示态势变化的动力学特征。对粗粒化后的状态序列采用加权马氏链预测模型,以此获得直观易于理解的结果。
1 安全态势复杂网络的构建
1.1 数据粗粒化处理
首先我们采用层次化评估模型[7]获取系统的安全态势值,系统的安全态势主要由服务层、主机层、系统层来反映。为此需计算服务层态势RS
[8]和主机安全态势
[9],最后按照主机在
RH
系统中的不同权重加权求和计算系统安全态势RL[9]。
安全态势值粗粒化处理是将安全态势时间序列符号化的过程[10]。我们用静态符号化思想将安全态势值RL划分为5个区间,把落在这5个区间的值分别用不同符号表示,即:
?
?????SR??
??????
ROYBG
Ri????
1
???Ri????211????Ri????22
1
????Ri???2
Ri????
(1)
优先出版
计 算 机 应 用 研 究
第32卷
式中?和?表示时间序列的均值和方差。R,O,Y,B,
G分别代表网络安全处于红色、橙色、黄色、蓝色、绿色预警
度进行研究。对于度的分布指网络中度为k的节点的概率p?k?随节点度k的变化规律,定义为:
状态,即严重、高危,中危,低危,安全。依据这一思想,我们将得到的安全态势序列RL转化为相应的符号序列
SR??s1s2s3
p?k??Ni/N (3)
其中Ni代表度值等于k的节点数,N代表节点总数。
两个节点i和j之间的距离为dij(即任意两个节点相互连接距离的平均值。即:
),平均路径长度L定义为任意两个节点之间?,?si??R,O,Y,B,G?? (2) 所要经过的连边数
1
?dij
NN?1i?j
在定义安全态势符号序列的基础上,对安全态势时间序列进行粗粒化处理,也就是区间同质划分,将整个系统区间分成有限个子区间,赋予每个子区间一个字符串,这样就把整个系统区间转换为一个符号序列。对粗粒化符号序列的研究等价于对相应时间序列的研究。 1.1
我们把L?
(4)
聚类系数描述网络中节点的邻点之间也互为邻点的比例,反映网络的紧密程度。整个网络的聚类系数为所有节点的聚类系数的平均值,考虑安全态势复杂网络是含权网络,则单个节点聚类系数定义为:
(5)
??S
2*i?1
,S
2i*
?
i的点强i的三角形
维度,RO体而言是以k的数,记
(6) ?i,j?的和
(7)
图1中的箭头方向性表示从一个时间到另一个时间状态维度的变化,虽然在理论上会产生25个状态维度,但是在本文实验仿真中仅仅会使用到其中的24个状态维度,其中一个状态维度不会在仿真实验中出现,至于其中一个状态维度之所以不出现与算法状态维度选择有关。
利用这24种变化模态构建安全态势随时间变化的加权网络,有向边定义为从前一时间段到后一时间段的模态连接,其中不同节点之间存在的多重连接数为两节点之间边的权数,由此可构建一个复杂网络[11-13]。
刻画复杂网络结构统计特性上主要有以下几个参数[14]:度和度分布、最短路径长度、聚类系数、中介中心性。 我们所构建的安全态势复杂网络是一个有向网络,其节点
度分为出度和入度,入度是指从某一模态指向该模态,节点出度指该模态向其它模态的直接转换。在本文中主要对节点的出
?2统计量检验具体步骤为:首先计算边际概率p.j,其为转移频数矩阵的第j列之和除以各行各列的总和所得的值。其中连接矩阵的维数为m,nij表示连接矩阵中状态转移频数, 即
m
mm
pj??nij/??nij
i?1
i?1j?1
(8)
其次计算统计量服从自由度为?m?1?2的?2分布,选定置信
2
度?,查表得???m?1?
m
m
?2?2??nilg?pij
i?1j?1
?,当样本足够大时,统计量
则该随机过程具有马/p?,若?????m?1??,
22
2
2
j
?
?
氏性。
传统的马尔科夫预测没有充分发挥历史数据的作用,因而,考虑先分别依其前面若干时点的状态对该时段状态进行预测; 然后,按前面各时段与该时段相依关系的强弱加权求和,这样可以达到充分、合理利用信息进行预测的目的。基于上述思路,加权马尔科夫链预测的步骤为:
(1) 计算态势序列各阶相关系数?k,即:
优先出版
n?kt?1
n
2
计 算 机 应 用 研 究
第32卷
?k???rt?r??rt?k?r?/??rt?r?其中rt表示采样点t的态势值,
t?1
以2字串的元结构作为网络的节点,则网络的有向连接形式为:
BR→BO→RY→BY→BY→RR→GY→BB→GB→OB→BR→BO→RY→BY→BY→RR→GY→BB→GB→OB→BR→···
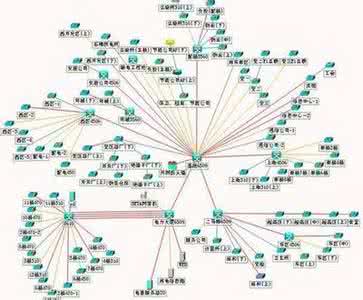
由此,我们构建体现符号序列内部各变化模态之间相互作用的有向含权网络图,如图2所示。
?k为第k阶自相关系数;为态势序列的均值,n为态势序列
的长度。
(2) 归一化各阶自相关系数,即:?k??k/??k将其作为各
k?1m
种滞时(步长)的马尔科夫的权重(m为按预测需要计算的最大阶
数);
(3) 分别以前面若干采样点各自的态势值为初始状态,结合其相应的状态转移概率矩阵即可预测出该时间点态势状态概率
,k?1m; pi?k?,i为状态,i?I,k为滞时(步长)
(4) 将同一状态的各预测概率加权和作为态势处于该状态的预测概率pi???ipi?k?,然后将其转化为归一化概率pi进行预
i?1m
测;
(5)
3 3.1 型,得到BR···
构成366测试集。
表1中的安全态势变化模态,前8个节点BB,YB,BY,RB,BO,BR,BG,GB度值比较大,这说明在安全态势复杂网络中,这些节点代表的安全态势变化模态在该网络中起到重要的直接关联作用,各种安全态势变化模态向这几个重要模态转
节点度大于k的概率
换,或者被这几个重要模态转换的频率较高,对网络节点度进行字频统计,发现在度数较大的前8个节点中,字符B出现的次数为9次,而代表安全状态为严重以上的R和O次数分别为2次和1次,说明网络大部分时间是处于低危和中危的状态。
图3给出节点累积度分布。在半对数坐标下,安全态势复
节点的度k
杂网络服从衰减的指数分布,意味着随机挑选的网络演化过程,这说明各种安全态势变化模态的发生有一定的随机性(即何时发生何种模态是不确定的),但各种安全态势变化模态出现次数
图3 节点累积度分布
优先出版
计 算 机 应 用 研 究
第32卷
在一个较长时间段内遵循较多的模态出现的概率较少,较少的模态出现的概率大。这从一方面反映了安全态势网络的无标度特征。
3.2.2 平均最短路径长度
根据公式4计算安全态势复杂网络的平均路径发现,各种
数的次,89.82%3.2.3 从图变化。这种特性为我们预测安全态势变化的群发性有一定的参考和帮助。由图4可知网络具有较大的聚类系数,而平均最短路径长度为1.875,说明模态之间转换大多表现为短程相关性,存在小规模的群簇,群簇内部 模态之间的关联较好,而群簇之间的关联则较差,这反映了网络的小世界特征。
并把它的BC1/3献率为3.3 根据第2节介绍的加权马氏方法对网络安全态势状态预测分析:
(1) 根据一步转移概率矩阵由公式可计算出?2?596.04,取??0.05,查表得?2?24?1??583.6,所以此过程具有马氏性,是
Lag
图5 安全态势值的自相关函数图
(3) 由于模型具有5阶相关性,借助建立的安全态势复杂网络分别计算步长为2步、3步、4步、5步的转移概率矩阵
pi?2?,pi?3?,pi?4?,pi?5?。同时得到预测概率:
?
2
?
马尔科夫过程。
(2) 由图5可知建立的模型具有显著的5阶相关性,将其各阶自相关系数归一化后作为各中时滞的马尔科夫链的权重,分别为:
?1?0.4,?2?0.27,?3?0.1,?4?0.07,?5?0.16
qi??1pi??2pi?2???3pi?3???4pi?4???5pi?5?。
(4) 利用前5个时间段状态对后一个状态进行预测,其预测结果和中值误差结果见表3。
优先出版
计 算 机 应 用 研 究
表3 预测结果统计表
第32卷
由上述预测结果可看出加权马氏链可以比较准确的对未来安全态势状态进行预测,准确率为75%。从中值误差可看出即使在预测正确的条件下误差最高也能到达14.2%,而在预测错误的状态中中值误差最小为6.01%,说明在粗粒化过程中状态区间划分,对结果有一定的影响。
[6] [5]
Environmental Science and Computer Engineering,2010 International Conference on.IEEE,2010:401-404.
卓莹,张强,龚正虎. 网络态势预测的广义回归神经网络模型[J]. 解放军理工大学学报(自然科学版),2012,13(2):147-151.
Chen J, Tu X. Network security risk assessment based on support vector machine[C]//Communication Software and Networks (ICCSN), 2011
4 结论
[7]
IEEE 3rd International Conference on.IEEE, 2011:184-187.
朱丽娜,[J].计算[8]
.[D].陈秀真,.[J]. 向,蒋静坪.时的符号化研究[J].模式识别与人工智
[11] ,郭琦. 国际石油价格复杂网络的动力学拓扑性质[J]. 物
59(7):4514-4523.
[12] ,龚志强,支蓉,封国林. 利用复杂网络研究中国温度序列的拓扑性
[J].物理学报,2008,57(11):7380-7389.
高湘峋,安海忠,方伟. 基于复杂网络的时间序列双变量 相关性波动研
Gruber
D.A
future
究[J].物理学报,2012,61(9):1-9.
[14] 汪小帆,李翔,陈关荣.复杂网络理论及应用[M].北京:清华人学出版
社,2006.
[15] 樊平毅.随机过程理论与应用[M].北京:清华大学出版社,2005.
本文基于复杂网络的网络安全态势预测机制来分析时间序列波动的动力学特征的问题,同时也可解决数值预测结果不利于直观理解的问题。通过仿真分析,安全态势复杂网络节点的累计度呈幂率分布,前8个节点(模态)的节点度值比较大,且这些模态中都包含表示低危状态的字符,安全态势网络部分节点的中介中心性能力较强, 前8个节点承担了网络56.57%中介中心性功能,平均路径长度1.875 ,距离是1和2占总数的89.82%,保障网络安全更加有效。 参考文献:
[1]
Bass
T,
ure.html,1999. [2]
李凯,曹阳. 基于ARIMA[J].计算机应用研究[3]
Man D, Wang Y, Wu YSecurity Situation[C]// and Software Engineering (CiSE), 2010 International Conference on.IEEE.2010:1-4. [4]
Jianfeng Dong. The Building of Network Security Situation Evaluation and Prediction Model based on Grey Theory [C]// Challenges in
 爱华网
爱华网