程与曲线
概念
在平面直角坐标系中,如果某曲线C上的点的坐标(x,y)都是方程F(x,y)=0的解;反之方程F(x,y)=0的解为坐标的点(x,y)都在曲线C上,那么方程F(x,y)=0叫曲线C的方程,曲线C叫方程F(x,y)=0的曲线。 已知曲线求它的方程的步骤 (1)建立适当坐标系,用(x,y)表示曲线上任一点P的坐标;(2)写出适合条件M的点P的集合
(3)用坐标表示条件M(P),列出方程;f(x,y)=0
(4)化方程f(x,y)=0为最简形式
(5)证明化简后的方程的解为坐标的点都是曲线上的点
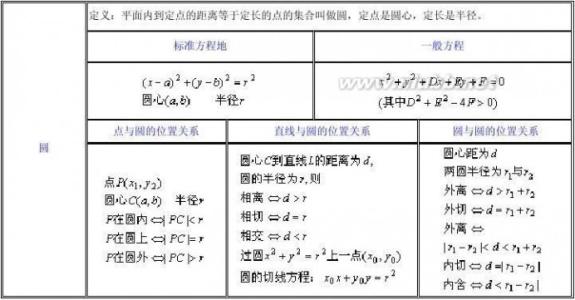
充分条件 < XMLNAMESPACE PREFIX ="V" />< XMLNAMESPACE PREFIX ="O" />必要条件 充要条件 ※中学数学公式定律手册※===>解析几何==>圆 定义:平面内到定点的距离等于定长的点的集合叫做圆,定点是圆心,定长是半径。标准方程地
一般方程点与圆的位置关系
直线与圆的位置关系
圆与圆的位置关系
※中学数学公式定律手册※===>解析几何==>椭圆椭圆
定义:平面内到两个定点F1,F2的距离之和等于一个常数(大于|F1F2|)的点的轨迹叫做椭圆,这两个定点叫做焦点,两定点间的距离叫做焦距。标准方程
图 象
焦 点
F1(-c,0) F2(c,0)
F1(0,-c) F2(0,-c)
焦 距
几何性质
范围
对称性 坐标轴是椭圆的对称由,原点是椭圆的对称中心。椭圆的对称中心叫做椭圆的中心。顶点
离心率 ※中学数学公式定律手册※===>解析几何==>双曲线曲线
定义:平面内到两个定点F1,F2的距离之差的绝对值是常数(大于|F1F2|)的点的轨迹叫做双曲线,这两个定点叫做焦点,两定点间的距离叫做焦距。标准方程
图 象
焦 点
F1(-c,0) F2(c,0)
F1(0,-c) F2(0,-c)
焦 距
几何性质
范围
对称性 坐标轴是椭圆的对称由,原点是椭圆的对称中心。椭圆的对称中心叫做椭圆的中心。顶点
渐近线 离心率 ※中学数学公式定律手册※===>解析几何==>抛物线抛物线
定义:平面内与一个定点F和一条定直线L距离相等的的轨迹叫做抛物线,点F叫做抛物线的焦点,直线L叫做抛物线的准线。标准方程
焦 点
准 线
图 象
几何性质
范围
对称性 曲线关于x轴对称,我们把抛物线的对称轴叫做抛物线的轴。顶点
坐标原点(0,0) 离心率 e=1※中学数学公式定律手册※===>解析几何==>直线
线
直线的方程
直线与x轴垂直不能用 直线与x轴垂直不能用 直线与坐标轴垂直不能用 直线与坐标轴垂直或过原点不能用 A、B不全为零 点到直线的距离两条直线的关系及条件
平 行
重 合
垂 直
斜交二直线的夹角 直线系 爱华网
爱华网