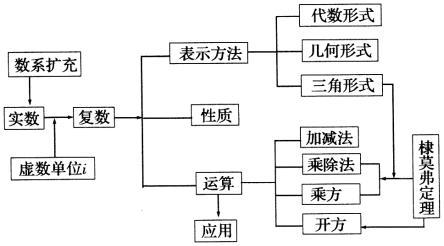
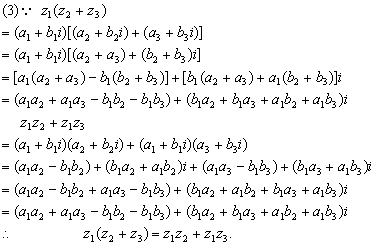导数的综合应用;极限;复数
二. 本周教学重难点:
1. 理解可能函数的单调性与其导数关系,会求函数的极值,最值
2. 掌握数列,函数极限的运算法则,会求数列函数极限,了解连续的意义
3. 了解复数的有关概念,能进行加、减、乘、除运算
【典型例题】
[例1] 已知a为实数,若在和上都递增,求的取值范围。
解:
令,即
∴
①
设 ∴
∴
当时,
当时, ∴
② 设
∴ ∴
当时,
当时, ∴
由①②知:
[例2] (且)在上是减函数,求的取值范围。
解:
令,或
∵ ∴
∴ ∵ ∴
[例3] 已知,函数
(1)当为何值时,取得最小值?证明你的结论。
(2)设在上是单调函数,求的取值范围。
解析:(1)对函数求导数,得
令,得
从而
解得,,其中
当变化时,、的变化如下表:
x
+
0
-
0
+
↗
极大值
↘
极小值
↗
当在处取到极大值,在处取到极小值。
当时,,,在上为减函数,在上为增函数。
而当时,;
当时,,所以当时,取得最小值。
(2)当时,在上为单调函数的充要条件是,
即,解得
综上,在上为单调函数的充分必要条件为,即的取值范围是。
[例4] 已知,,若,且存在单调递减区间,求的范围。
解:时,
令,即有解即可
∴
∵ ∴ (*)
设, ∴
∵ ∴
∵ (*)有解即可 ∴
当时,
∵ ∴ 不可能小于0
∴ 又∵ ∴ 且
[例5] 把边长为60cm的正方形铁皮的四角切成边长为xcm的相等的正方形,然后折成一个高度为xcm的无盖的长方体的盒子,要求长方体的高度与底面边长的比值不超过常数,问x取何值时,盒子的容积最大,最大容积是多少?
解:设长方体高为xcm,则底面边长为
长方体容积
∵ ∴ ,即函数定义域为
令,解得,(不合题意舍去),于是
x
(0,10)
10
(10,30)
+
0
-
↗
↘
① 当即时,在时,取得最大值为
② 当即时,在时,取得最大值
[例6] 已知,求。
解:∵
∴ 为方程的根,
又
∴ ∴ ,
[例7] 是否存在常数使等式
对一切正整数成立?证明你的结论。
解:分别将代入
∴
下面用数学归纳法证明
(1)当时,成立
(2)假设时等式成立
当时,
左
由(1)(2)知等式对一切成立
[例8] m取何实数时,复数是实数?是虚数?是纯虚数?
解:① 为实数
∴
② 为虚数
∴ 且
③ 为纯虚数
∴ 或
【模拟试题】
一. 选择题
1. 已知,函数在上是单调增函数,则的最大值是( )
A. 0 B. 1 C. 2 D. 3
2. 已知曲线过点,则这一曲线在该点的切线方程是( )
A. B.
C. D.
3. 已知(m为常数)在上有最大值6,那么此函数在上的最小值为( )
A. –34 B.-29 C.-5 D.-11
4. 函数,其中为实数,当时,( )
A. 是增函数 B. 是减函数
C. 是常数函数 D. 既不是增函数也不是减函数
5. 已知函数,则( )
A. 极大值为5,极小值为
B. 极大值为5,极小值为
C. 极大值为5,无极小值
D. 极小值为,无极大值
6. 函数的极值点是( )
A. B.
C. 或 D.
7. 观察函数:① ;② ;③ ;④ 。
当时极限值为1的是( )
A. ①③ B. ②③ C. ③④ D. ①④
8. 等于( )
A. B. C. D.
二. 解析题
1. 已知函数。
(1)若在实数集R上单调递增,求实数的取值范围。
(2)是否存在实数,使在上单调递减?若存在,求出的取值范围;若不存在,请说明理由。
(3)证明的图象不可能总在直线的上方。
2. 已知,求的单调区间。
3. 某厂生产某种产品的固定成本(固定投入)为2500元,已知每年生产x件这样的产品需要再增加可变成本(元),若生产出的产品都能以每件500元售出,要使利润最大,该厂应生产多少件这种产品?最大利润是多少?
【试题答案】
一.
1. D
解析:,因为在上单调递增,所以,即,故。
2. B
解析:∵ 曲线过点
∴ 又 ∴
∵ ∴ 切线方程为
∴ 选B
3. A
解析:
由得或2
∵ ,,
显然
∴ ,最小值为
4. A
解析:,其判别式
∴ 时恒有成立
∴ 为增函数
5. C
解析:令,得或
∵ ∴
当时,
而当时,
∴ 为的极大值点
当时,
6. D
解析:由,得或
当时,;时,
∴ 不是极值点,同理也不是的极值点,为的极值点,故选D。
7. D
解析:经计算:①的极限为1,②的极限为0,③的极限为,④的极限为1,所以选D
8. B
解析:∵ ∴
二.
1. 解析:(1)由已知 ∵ 在上是单调增函数
∴ 在上恒成立,即对恒成立
∵ ∴ 只需
又时,,在R上是增函数
∴
(2)由在上恒成立
得,恒成立
∵ ∴ ∴ 只需
当时,,在上,
即在上为减函数 ∴
故存在实数,使在上单调递减
(3)证明∵
∴ 的图象不可能总在直线上方
2. 解析:
(1)当时,若,;若,
所以当时,在内为减函数,在内为增函数
(2)当时,由
解得或
由,解得
所以时,在内为增函数,在内为减函数,在内为增函数
(3)当时,由,解得,由,解得或,所以当时,在内为减函数,在内为增函数,在内为减函数。
3. 解析:设该厂生产x件这种产品的利润为元,则
令,得(件)
又当时,;
当时,,所以是的极大值点。
当时,元
因此,要使利润最大,该厂应生产这种产品60件,最大利润为9500元
 爱华网
爱华网