本书阐明数学建模和计算建模在各个学科中的应用。本书的重点在于说明数学建模和计算建模具有跨学科的性质,各章的作者都是自然和社会科学、工程学和艺术等领域的国际级专家,为读者提供当代在发展数学建模和计算机实验的方法论方面的丰富的成果。本书也是关于应用数学和计算数学的方法、思想和工具等方面很有价值的导引书,借助这些方面的知识来解决自然科学、社会科学、工程和技术等方面的问题。
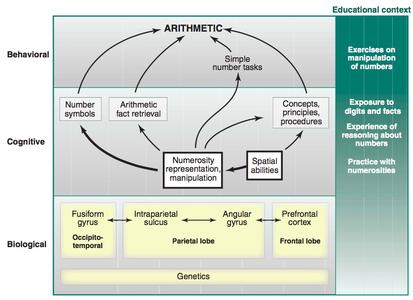
本书的特点在于:(1) 严格的数学步骤和实例――数学创新和发现的驱动力;(2)从广泛学科中挑选的众多实例,重在说明应用数学和数学建模的多学科应用和普适性;(3) 来自人类知识各方面发展中既有理论也有应用的原创性结果;(4)促进数学家、科学家和工程师之间进行交叉学科相互作用的讨论。
对于从事数学和统计科学、模化和模拟、物理学、计算科学、工程学、生物和化学、工业和计算工程等领域的专业人员来说,这是一本理想的参考书。本书也可当作数学建模、应用数学、数值方法、运筹学以及优化等方面的大学课程的教科书。
本书共分五部分,12章。第一部分 引论,含第1章:1.在理解自然、社会和人造世界中数学模型的普适性。第二部分 在物理学和化学中的高等数学模型和计算模型,含第2-4章:2.磁涡,Abrikosov 晶格,以及自同构函数;3.在Cholesky分解的局部关联量子化学架构中的数值挑战;4.量子力学中的广义变分原理。第三部分 在生命科学和气候科学应用中的数学模型和统计模型,含第5-6章:5.具有药物敏感、出现多重耐药以及广泛耐药株的结核病的传播模型;6.着眼于抗菌素耐药性而对更加综合的传染病进行建模的需要。第四部分 科学和工程中的数学模型与分析,含第7-10章:7.动力学系统中由数据驱动的方法:量化可预报性以及提取时空图案;8.求解Banach空间中非线性反问题进行正则化的光滑度概念;9.一阶对称具有约束的双曲型系统的初值问题和初边值问题;10.信息集成,组织和数值调和分析。第五部分 社会科学和艺术中的数学方法,含第11-12章:11.满意认可的选举;12.使用几何量化对音乐韵律变化的建模
谈庆明,教授
(中国科学院力学研究所)
爱华网本文地址 » http://www.aihuau.com/a/314551/747744132096.html
更多阅读

1 数学建模竞赛是什么?路漫漫其修远兮,吾将上下而求索数学建模竞赛,就是在每年叶子黄的时候(长沙的树叶好像一年到头都是绿的)开始的一项数学应用题比赛。大家都做过数学应用题吧,不知道现在的教育改革了没有,如果没有大变化,大家都应该做过
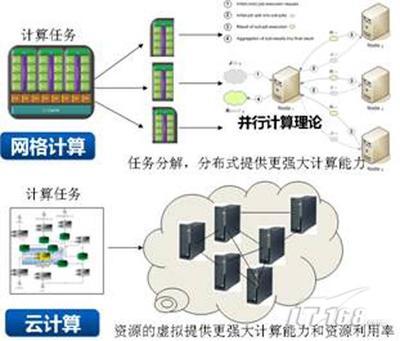
云计算与分布式计算区别分布式计算是指在一个松散或严格约束条件下使用一个硬件和软件系统处理任务,这个系统包含多个处理器单元或存储单元、多个并发的过程、多个程序。一个程序被分成多个部分,同时在通过网络连接起来的计算机上运

建筑工地用电负荷计算及变压器容量计算与选择(之三教材版) (2009-8-1322:15:51)分类:建筑设计与施工 标签:搜房博客| 建筑工地用电负荷计算及变压器容量计算与选择(教材版)一、土建施工用电的需要系数和功率因数用电设备名称用电设备

孙子兵法与三十六计(视频全集1~36集)渴望美好 网摘一、上屋抽梯

《孙子兵法与三十六计》读后感怀着好奇的心理我阅读了这一本世界三大兵书之一,享有“兵学圣典”的美誉的《孙子兵法与三十六计》,它是我国古代卓越兵家的智慧结晶,是世界军事谋略学的宝贵遗产之一。《孙子兵法》的部分里可分为计篇﹑

 爱华网
爱华网



