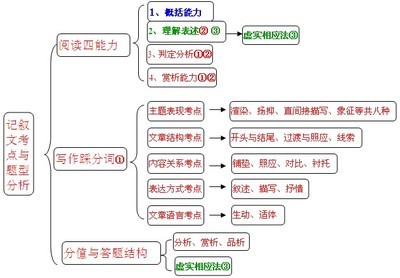
二项式定理
二. 本周教学重、难点:
掌握二项式定理和展开式的性质,并能用它们计算,证明一些问题
【典型例题】
[例1] (1)求的展开式中的常数项。
(2)求展开式中的有理项。
解:(1),
令 ∴
(2)
令即,
∴ 或9
当时,,
当时,,
[例2] 求展开式中的系数
解:因为的通项为,
的通项为,,令,则
,,,
所以的系数为
[例3] 求展开式中含项的系数
解:
而其中的通项为,的通项为
所以的通项为,其中,且
由已知,,所以,从而
当时,,这时;
当时,,这时;
当时,,这时;
所以展开式中含项的系数为
[例4] 求的展开式中项。
解:方法一:原式
的通项,
∴
当时 ∴ ∴ 或
∴ 含项:
方法二:2个,1个
4个
∴
[例5] (1)求展开式中系数最大的项;(2)求展开式中系数最大的项。
解:(1)设项系数最大,则有
即
解得 又∵ ∴
∴ 系数最大项为
(2)展开式中共有8项,系数最大项必为正项,即在第一、三、五、七这四项中取得,又因括号内两项中后项系数绝对值大于前项系数的绝对值,故系数最大项必在中间或偏右,故只需要比较和两项系数大小即可。
∴ 系数最大的项是第五项,
[例6] 的展开式中第6项与第7项的系数相等,求展开式中二项式系数最大的项。
解:
∴ ,即
∴ 解得
∴ 展开式中二项式系数最大的项是中间一项
[例7] 若,求
(1);
(2);
(3)。
解:(1)令,则
令,则①
∴
(2)令,则②
由,得
(2)由,得
[例8] 求证:能被64整除
证明:∵
又是整数
∴ 能被64整除
[例9] 求证:有。
证:∵
∴ 左
右
[例10] 求
解:原式
[例11] 若,,展开按m的降幂排列第二项不大于第三项,求m的取值范围。
解: ∴
又∵ ∴
【模拟试题】
一. 选择题
1. 在的展开式中,含项的系数是( )
A. B. 5 C. D. 10
2. 在的展开式中的系数是( )
A. B. 14 C. D. 28
3. 若展开式中含的项的系数等于含x的项的系数的8倍,则n等于( )
A. 5 B. 7 C. 9 D. 11
4. 若展开式中存在常数项,则n等于( )
A. 8 B. 9 C. 10 D. 12
5. 的展开式中有且仅有5个有理项,则最小自然数n等于( )
A. 11 B. 12 C. 13 D. 14
6. 若,则等于( )
A. 1 B. C. 2 D.
7. 设二项式的展开式的各项系数的和为P,所有二项式系数的和为S。若有P+S=272,则n等于( )
A. 4 B. 5 C. 6 D. 8
8. 展开式中整理后的常数项是( )
A. 32 B. C. 70 D. 38
二. 解答题
1. 设函数(为实常数),若的展开式中的系数为,求的值。
2. 已知展开式中常数项为1120,为常数,求展开式中各项系数的和。
【试题答案】
1. C
解析:项的系数为,选C。
2. B
解析:由 ∴ 的系数为14
3. A
解析:含项的系数为,含x项的系数为,由题意得
或(舍)
4. C
解析:本题考查二项式定理,展开式中的第项为
由题意可知
∵ ∴ 为3的倍数 ∴ n为5的倍数
5. B
解析:∵ ,设为有理项,则,且,
∴ 要求n的最小值,只要求出r的最大值即可
又∵ 只有5个有理项 ∴
∴ ,从而
故选B
6. D
解析:令,得,令,得
∴
7. A
解析:若,有,,令,得,又
或(舍去)
∴ ,故选A
8. D
解析:展开式的通项
由,得,故展开式中常数项为
同理,可求的展开式中的常数项为70
∴ 所求常数项为
二.
1. 解析:
由 ∴
∵ ∴
2. 解析:
∴ 当时,为常数项
∴ ∴ ∴
∴ 展开式中各项系数之和为:
① 时,令 ∴
② 时,令 ∴
 爱华网
爱华网