相关解答一:如何求一个曲线的切线方程
曲线C:y=f(x),曲线上点P(a,f(a))
f(x)的导函数f '(x)存在
(1)以P为切点的切线方程:y-f(a)=f '(a)(x-a)
【例如:已知函数f(x)=(3x^2+6x-6)/(x-1)求函数f(x)在点(-1,9/2)处的切线方程;
f(x)=(3x^2+6x-6)/(x-1)=[(3x^2-3x)+(9x-9)+3]/(x-1)=(3x+9)+3/(x-1)
f(-1)=(3-6-6)/(-1-1)=9/2,即点(-1,9/2)在函数图像上,
f′(x)=3-3/(x-1)^2,
f′(-1)=3-3/(-1-1)^2=9/4,
所以切线方程为 y-9/2=(9/4)(x+1),
即y=(9/4)x+27/4.
(2)若过P另有曲线C的切线,切点为Q(b,f(b)),
则切线为y-f(a)=f '(b)(x-a),也可y-f(b)=f '(b)(x-b),并且[f(b)-f(a)]/(b-a)=f '(b)
【例如:求双曲线y=1/x过点(1,0))的切线方程.
对双曲线y=1/x,f(x)=1/x,导函数f′(x)=-1/(x^2),
因为f(1)=1/1=1≠0,所以点P(1,0)不在此双曲线上
设过P(1,0)的直线与双曲线相切于点T(a,f(a)),
这时切线的斜率为k=[f(a)-0]/(a-1)=f′(a)=-1/(a^2),
即(1/a)/(a-1)=-1/(a^2),解得a=0(这时f(a)=f(0)没有定义,舍去)或a=1/2
所以切线方程为y-0=(1/2)(x-1)
即x-2y-1=0
相关解答二:求 曲线的切线方程
由题意:
对函数求导,这是复合函数求导。
令t=x+1,则原函数由y=1/t集合t=1+x复合而成
y'=(1/t)'*(1+x)'=-1/t^2*1=-1/(1+x)^2
令x=1,y'=-1/2^2=-1/4
所以在A点处的切线斜率为-1/4,
所以切线方程:y=-1/4 *(x-1)+1/2,即y=-x/4+3/4
相关解答三:如何求一条曲线在某一点处的切线方程
主要是用导函数做的,对原函数求导,把切点的横标代入导函数,求的切线的斜率即可求切线方程
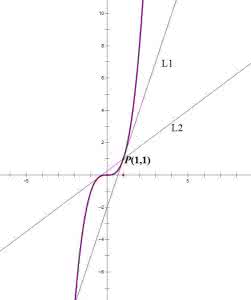
相关解答四:已知曲线一点求切线方程
x=1, y=0
y'(x)=3x^2, y'(1)=3
因此过点(1,0)的切线为: y=3(x-1)
相关解答五:曲线过某一点的切线方程如何求
先把曲线方程整理成y=f(x)的形式,然后对x求导函数,切点横坐标x0对应的导函数值就是切线的斜率k,然后写出点斜式方程:y-y0=k(x-x0)即可.
相关解答六:求点到曲线的切线方程
切线是与椭圆有一个交点的直线,可联立方程组,求判别式
设直线是y=k(x-4),带入椭圆方程整理得
(4k^2+3)x^2-32k^2x+64k^2-12=0
判别式为(32k^2)^2-4(4k^2+3)*(64k^2-12)=0
整理得9-36k^2=0
解方程得k=1/2或-1/2
用导数也行,你做做看
相关解答七:求曲线在某点处的切线方程和求过某点的曲线的切线方程有什么区别,后者怎么做
在某点处的切线则这点是切点
过某点的曲线的切线
这不一定是切点
设切点是[a,f(a)]
则切线斜率是f'(a)
所以y-f(a)=f'(a)=(x-a)
把嗲代入,解出啊
相关解答八:求曲线的切线斜率和切线方程
例题1.曲线y=2x^2+3在点(-1,5)处的切线的斜率是_______________?
直接求导数,得y'=4x,代入x=-1得y'=-4,所以斜率为-4
例题2.曲线y=x^3+1在点(1,2)处的切线方程是__________________?
先求导,y'=3x^2,代入x=1得y'=3
令切线方程为y=3x+b,3为刚刚求得的斜率,因为点(1,2)既经过原直线又经过切线,代入求得b=-1
所以切线方程为y=3x-1
相关解答九:知道一条曲线,和曲线上一点,怎样求过这点的切线方程
曲线C:y=f(x),曲线上点P(a,f(a))
f(x)的导函数f '(x)存在
(1)以P为切点的切线方程:y-f(a)=f '(a)(x-a)
【例如:已知函数f(x)=(3x^2+6x-6)/(x-1)求函数f(x)在点(-1,9/2)处的切线方程;
f(x)=(3x^2+6x-6)/(x-1)=[(3x^2-3x)+(9x-9)+3]/(x-1)=(3x+9)+3/(x-1)
f(-1)=(3-6-6)/(-1-1)=9/2,即点(-1,9/2)在函数图像上,
f′(x)=3-3/(x-1)^2,
f′(-1)=3-3/(-1-1)^2=9/4,
所以切线方程为 y-9/2=(9/4)(x+1),
即y=(9/4)x+27/4。
zhidao.baidu.com/...oldq=1】
(2)若过P另有曲线C的切线,切点为Q(b,f(b)),
则切线为y-f(a)=f '(b)(x-a),也可y-f(b)=f '(b)(x-b),并且[f(b)-f(a)]/(b-a)=f '(b)
【例如:求双曲线y=1/x过点(1,0))的切线方程。
对双曲线y=1/x,f(x)=1/x,导函数f′(x)=-1/(x^2),
因为f(1)=1/1=1≠0,所以点P(1,0)不在此双曲线上
设过P(1,0)的直线与双曲线相切于点T(a,f(a)),
这时切线的斜率为k=[f(a)-0]/(a-1)=f′(a)=-1/(a^2),
即(1/a)/(a-1)=-1/(a^2),解得a=0(这时f(a)=f(0)没有定义,舍去)或a=1/2
所以切线方程为y-0=(1/2)(x-1)
即x-2y-1=0
zhidao.baidu.com/...oldq=1】
相关解答十:知道一条曲线,和曲线上一点,怎样求过这点的切线方程
记曲线为f(x),
点M(a,b).在曲线上,则可直接写出过M的切线为:y=f'(a)(x-a)+b
点M(a,b).不在曲线上,则过M点且与曲线相切的直线为:y=k(x-a)+b,需要求k,令此切线与曲线的切点为xo,k=f'(xo),xo为方程 f'(x)(x-a)+b=f(x),的解.解此方程即得xo,进而k=f(x0).注意可能有多个xo解.
百度搜索“爱华网”,专业资料,生活学习,尽在爱华网
 爱华网
爱华网