"数学是锻炼思维的体操",逻辑推理推理问题的趣味性很强,不需要专门的数学知识,而是考察大家的思维能力、判断能力。推理论证的才能不是天生的,而是在不断的实践活动中逐渐锻炼、培养出来的。
小升初中很多学校也把逻辑推理当作考察学生综合实力的一种题型,也是人大附中必考的题型。本人以讲解典型题型方式,通过归纳、总结提供给大家逻辑推理在小学奥数中的常用方法。
典型例题:一、条件分析型
问题如下:有三个盒子:一个装两个红球,一个装两个白球,还有一个装着一红一白两个球,三个盒子都盖着盖子,盖子上贴着说明盒内装着是什么颜色球的标签,但全部贴错了,你能否从一个盒子里摸出一个球,就准确地判断出3个盒子里各装的是什么球?
如果从贴有"红红"或"白白"的盒里那一个球,这样判断不出来到底是两红,两白还是一红一白。所以从贴有"红白"的盒子里拿,如果拿出的球是红色,则全红;如果拿出的球是白色,则全白。再审题,题中有一个"全部贴错",意思是没有一个贴对。假设我们由"红白"盒子里拿出的是红球,则将贴有"红白"和"红红"的盒子互换标签,再将"红白"和"白白"互换标签,结果就出来了。
典型例题:二、假设推理型
问题如下:甲、乙、丙三人,一个总说谎,一个从不说谎,一个有时说谎。有一次谈到他们的职业。
甲说:"我是油漆匠,乙是钢琴师,丙是建筑师。"
乙说:"我是医生,丙是警察,你如果问甲,甲会说他是油漆匠。"
丙说:"乙是钢琴师,甲是建筑师,我是警察,"
你知道谁总再说谎吗?
解题方法
问题如下:先假设甲总说谎,乙有时说谎,丙从不说谎。甲说的全是假话,乙说:"我是医生,丙是警察,你如果问甲,甲会说他是油漆匠。"这个话还判断不出他们的准确职业。看下一句,丙说:"乙是钢琴师,甲是建筑师,我是警察。"丙是从不说谎的,但是他和丙都说了乙是钢琴师,所以推出矛盾。甲不总说谎。再设乙总说谎,甲从不说谎,丙有时说谎。乙总说谎,说明乙不是医生,丙不是警察,乙又说你如果问甲,甲会说他是油漆匠,问题是你没问他呢,所以这句也是假话,丙有时说谎,通过上面的判断,丙最后两句说了谎,第一句是真话。假设成立,说以乙总说谎。
典型例题:三、数学计算型。
问题如下:四对夫妇做在一起闲谈。四个女士中,A吃了三个梨,B吃了两个,C吃了四个,D吃了一个;四个男士中,甲吃的和妻子一样多,乙吃的是妻子的两倍吃,丙的是妻子的三倍吃,丁的是妻子的四倍。四对夫妇共吃了32个梨。问:丙的妻子是谁?
解题方法
男士共吃:32-(3+2+4+1)=22(个)
每个男士吃的是妻子的倍数:1倍、2倍 、3倍 、 4倍 。
只要通过这"1倍、2倍 、3倍 、 4倍"和他们妻子吃梨的个数凑出来22就行。
4倍的一定是B,3倍的可能是D、A,如果A是三倍的话,加起来就超22所以,D是3倍。剩下的就是B为4倍,C为2倍,如果换一下就超22了。
通过上面结论,我列出了下表:
A B C D
个数 3 2 4 1
倍数 1 4 2 3
男个数 3 8 8 3
总个数 6 10 12 4
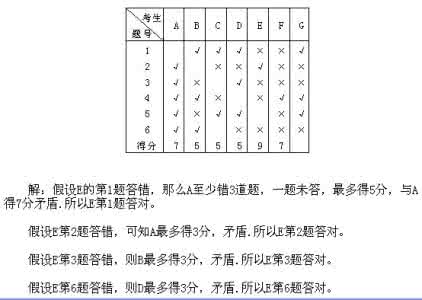
检验:6+10+12+4=32 正确
所以丙的妻子是D。
典型例题:四、计算机程序解题的初探。
上题其实是采用不定方程确定出满足条件的解,计算机程序中用多重循环求解是不错的方法。具体如下
首先明确解题思路:即上题中提到的总梨数减去妻子们吃梨的数量就是男士们吃的梨数量,而男士们吃的梨数量又对应各自妻子吃梨的不同倍数,这样们可以得到1个含有4个未知数的不定方程,求得满足方程的丙对应的数就是了
确定算法,用a、b、c、d变量分别代表甲、乙、丙、丁他们妻子吃梨的个数,满足题意的算法:a+2b+3c+4d=22
a、b、c、d最小是1,最多是4,所以循环的上下限可以确定为1,4
选用计算机语言编写程序并上机调试运行,现在用 Foxpro语言编写。
for a=1 to 4
for b=1 to 4
for c=1 to 4
for d=1 to 4
s=a+2*b+3*c+4*d
if s=22
@0,0 clear
do case
case c=1
@5,20 say '丙的妻子是D'
case c=2
@5,20 say '丙的妻子是B'
case c3=
@5,20 say '丙的妻子是A'
case c=4
@5,20 say '丙的妻子是C'
endcase
return
endif
endfor
endfor
endfor
endfor
运行后的结果:丙的妻子是D (见下抓屏幕中的结果)
其实程序可以优化与美化的,现在只是简单的演示,也可以用其它任何一种语言实现。
 爱华网
爱华网