职业能力探索小结 第二十四章　圆 小结和能力训练

　　【课标要求】

考点

课标要求

知识与技能目标

了解

理解

掌握

灵活应用

圆

圆及其有关概念

∨

弧、弦、圆心角的关系，点与圆以及圆与圆的位置关系

∨

圆周角与圆心角的关系，直径所对圆周角的特征

∨

三角形的内心和外心

∨

切线的概念，探索切线与过切点的半径之间的关系

∨

判定圆的切线，会过圆上一点画圆的切线

∨

计算弧长及扇形的面积，会计算圆锥的侧面积和表面积

∨

　　【知识梳理】

　　1．与圆有关的概念：正确理解弦、劣弧、优弧、圆心角等与圆有关的概念，并能正确分析它们的区别与联系。

　　2．与圆有关的角：掌握圆周角和圆心角的区别与联系，将圆中的直径与90°的圆周角联系在一起，一般地，若题目无直径，往往需要作出直径。

　　3．圆心角、弧、弦之间的关系与垂径定理：定理和结论是在圆的旋转不变性上推出来的，需注意“在同圆或等圆中”中这个关系。

　　 4．与圆有关的位置关系：了解点和圆、直径和圆、圆和圆共有几种位置关系，并能恰当地运用数量关系来判断位置关系是学习的关键。

　　5．切线长定理：切线长定理是圆的对称性的体现，它为说明线段相等、角相等、弧相等、垂直关系提供了理论依据。

　　【能力训练】

　　一、选择题

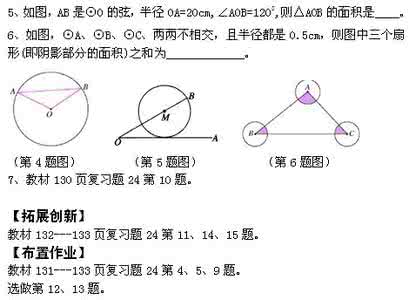
　　1. 如图，在半径为5的⊙O中，如果弦AB的长为8，那么它的弦心距OC等于（    ）

    A. 2        B. 3            C. 4                D. 6

　　2.已知O为△ABC的外心，∠A＝60°，则∠BOC的度数是（   ）

  A．外离   B．外切   C．相交             D． 内切

　　3．在半径为1的⊙O中，120?的圆心角所对的弧长是（    ）

　　A．    B． C．   D．     

　　4．已知两圆的半径分别是2和3，两圆的圆心距是4，则这两个圆的位置关系是   （   ）

　　 A．外离       B．外切       C．相交       D．      内切      

5．如图，⊙0的直径AB=8，P是上半圆(A、B除外)上任一点，∠APB的平分线交⊙O于C，弦EF过AC、BC的中点M、N，则EF的长是(    )．

 　　 A．4    B．2  C．6    D．2

　　6．若⊙O所在平面内一点P到⊙O上的点的最大距离为a，最小距离为b(a>b)，则此圆的半径为

A.                             B.                       C. 或         D. a+b或a-b

　　二、填空题

　　1．如果正多边形的一个外角为72°，那么它的边数是___________

　　2．已知圆锥的底面半径是2，母线长是4，则圆锥的测面积是               

　　3．如图，⊙O是等边三角形ABC的外接圆，D、E是⊙O上两点，则∠D＝   °，∠E＝       °

　　4．如图,正方形ABCD内接于⊙O,点E在弧AD上,则∠BEC=_______

　　三、解答题

　　1．已知：在Rt△ABC中，∠ABC＝90°，D是AC的中点，⊙O经过A、D、B三点，CB的延长线交⊙O于点E（如图1）。

    在满足上述条件的情况下，当∠CAB的大小变化时，图形也随着改变（如图2），在这个变化过程中，有些线段总保持着相等的关系。

    （1）观察上述图形，连结图2中已标明字母的某两点，得到一条新线段，证明它与线段CE相等；

    （2）在图2中，过点E作⊙O的切线，交AC的延长线于点F。

    ①若CF＝CD，求sin∠CAB的值；

    ②若，试用含n的代数式表示sin∠CAB（直接写出结果）。

    （1）连结__________________求证：_________＝CE

          证明：

    （2）解：①

②_____________（）

2．如图，在⊙O中，弦AB与DC相交于E，且AE＝EC，求证：AD＝BC．

3．如图，已知BC是⊙O的直径，AH⊥BC，垂足为D，点A为弧的中点，BF交AD于点E，且BEEF=32，AD=6.

(1) 求证：AE=BE；

(2) 求DE的长；

(3) 求BD的长 .

　　4．右图的花环状图案中,ABCDEF和A1B1C1D1E1F1都是正六边形.

　　（1）求证:∠1=∠2;

（2）找出一对全等的三角形并给予证明

　　5．如图M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDE…的边AB、BC上的点，且BM=CN，连结OM、ON。

　　（1）求图1中∠MON的度数；

　　（2）图2中∠MON的度数是_________，图3中∠MON的度数是_________；

　　（3）试探究∠MON的度数与正n边形边数n的关系（直接写出答案）。

　　13.在坐标平面内，半径为R的⊙O与x轴交于点D（1，0）、E（5，0），与y轴的正半轴相切于点B。点A、B关于x轴对称，点P（a，0）在x的正半轴上运动，作直线AP，作EH⊥AP于H。

（1）       求圆心C的坐标及半径R的值；

（2）       △POA和△PHE随点P的运动而变化，若它们全等，求a的值；

（3）       若给定a=6，试判定直线AP与⊙C的位置关系（要求说明理由）。

　　参考答案：

　　一、选择题1．B；2．A；3．B；4．C；5．A；6．C

　　二、填空题

　　1．5；　　　2．8π；　　 3．60，120；　　　4．45

　　三、解答题

　　1．略；2．提示：三角形全等；3．提示：证明弦所对的角相等；4．答案多样，正确就可以；5．提示：连结OB、OC；6．C（3，），相切。

爱华网本文地址 » http://www.aihuau.com/a/319551/758314759649.html