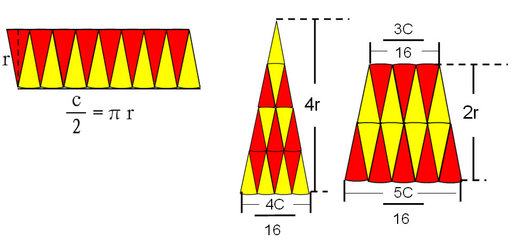
设△ABC的三边为a,b,c,由解直角三角形易得三边上的高ha,hb,hc,根据面积公式,可以推导出另一面积公式. 由此公式,可以直接计算已知两边及夹角的三角形面积,并解决一些与面积相关的问题.
一、应用面积公式,推导正弦定理
例1设△ABC的三边为a,b,c,求证:.
证明:由三角形面积公式,得到,
即.
上式同时除以abc,得到.
所以,.
点评:三角形面积公式由直角三角形的边角关系表示出各边上的高之后再推导出来,再运用它推导正弦定理,实质就是教材中正弦定理推导过程的简化.
二、活用代数变形,推导海伦公式
例2 △ABC的三边为a,b,c,设,求证:.
证明:==
=
=
=
=
=
= .
点评:此例的结论,就是海伦公式,可以由三角形的三边a、b、c直接求出三角形的面积. 海伦公式据说是由古希腊数学家阿基米德解决的,但最早出现于古希腊数学家海伦(Heron)的著作《测地术》中,公式的形式漂亮,且便于记忆. 我国大数学家秦九韶在也发现与海伦公式本质上相同的“三斜求积”公式,并记载于他写的《数书九章》中. 如果由三角形面积和,得,,根据,整理后也可得到海伦公式.
三、结合面积公式,研究三角问题
例3 在△ABC中,角A、B、C所对的边分别是a、b、c.
(1)若a=4,b=5,S=5,求c的长度;
(2)若三角形的面积S=,求∠C的度数;
(3)若a、b、c成等比数列,且a2-c2=ac-bc,求∠A的大小及的值.
解:(1)∵S=absinC,∴sinC=,于是∠C=60°或∠C=120°.
又∵c2=a2+b2-2abcosC,
当∠C=60°时,c2=a2+b2-ab,c=;
当∠C=120°时,c2=a2+b2+ab,c=.
∴ c的长度为或.
(2)由S=,得absinC=. ∴ tanC=1,得C=.
(3)∵a、b、c成等比数列,∴b2=ac.
又a2-c2=ac-bc,∴b2+c2-a2=bc.
在△ABC中,由余弦定理得
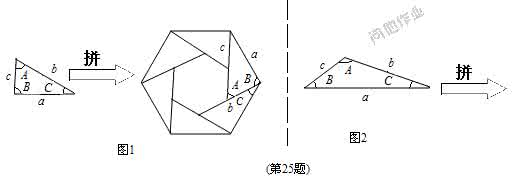
cosA===,∴∠A=60°.
在△ABC中,由面积公式得bcsinA=acsinB.
∴ bcsinA=b2sinB, 则=sinA=.
点评:解三角形时,需认真分析题中已知条件中边与角之间的关系,根据条件合理选用正弦定理或余弦定理,结合三角形的面积公式来解决问题.
四、综合面积公式,探讨数学领域
例4 已知圆内接四边形ABCD的边长AB=2,BC=6,CD=DA=4. 求四边形ABCD的面积.
解:如图,连结BD,则四边形面积
S=S△ABD+S△CBD=AB·ADsinA+BC·CDsinC
∵ A+C=180°, ∴sinA=sinC,
∴ S=(AB·AD+BC·CD)·sinA=16sinA.
在△ABD中,由余弦定理得BD2=22+42-2·2·4cosA=20-16cosA.
在△CDB中,BD2=52-48cosC, ∴20-16cosA=52-48cosC.
又cosC=-cosA,∴cosA=-, ∴A=120°,得S=16sinA=8.
点评:在印度婆罗摩笈多(约593-665后)的书中,出现了有圆内接四边形的求积公式(其中a,b,c,d为四边形的四条边,p为四边形的周长之半). 当d=0时,这个公式即为海伦公式. 推广到任意四边形,则得到婆罗摩笈多公式.
三角形的面积公式有许多,例如已知三角形的三边a、b、c及外接圆、内切圆的半径为R,r,则有S△=abc/4R与.
又如,在△ABC中,若=(),= (),则△ABC的面积为S=. 此三角形面积的向量公式可如下证明.
证明:
由上例公式,不必求三角形的边长和角度,只要知道任意两边所对应的向量即可,而其向量在已知三角形三个顶点的坐标时不难求得. 由此,我们知道三角形三个顶点的坐标,也可以得到如下面积公式.
, ,则
= .
以上我们探讨了各面积公式之间的相互联系,灵活运用三角形的面积公式,能帮助我们解决许多解三角形的问题.
2006-12-30 原创作品 爱华网
爱华网