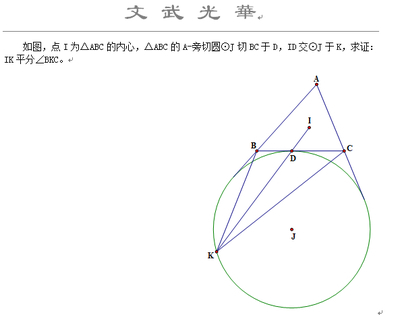
一道竟赛题的思考湖北省黄石市下陆中学702班 李 杰 指导老师:周国强#TRS_AUTOADD_1311840951384 {MARGIN-TOP: 0px; MARGIN-BOTTOM: 0px}#TRS_AUTOADD_1311840951384 P {MARGIN-TOP: 0px; MARGIN-BOTTOM: 0px}#TRS_AUTOADD_1311840951384 TD {MARGIN-TOP: 0px; MARGIN-BOTTOM: 0px}#TRS_AUTOADD_1311840951384 DIV {MARGIN-TOP: 0px; MARGIN-BOTTOM: 0px}#TRS_AUTOADD_1311840951384 LI {MARGIN-TOP: 0px; MARGIN-BOTTOM: 0px}/**---JSON--{"":{"margin-top":"0","margin-bottom":"0"},"p":{"margin-top":"0","margin-bottom":"0"},"td":{"margin-top":"0","margin-bottom":"0"},"div":{"margin-top":"0","margin-bottom":"0"},"li":{"margin-top":"0","margin-bottom":"0"}}--**/DIV.MyFav_1310453216462 P.MsoNormal{TEXT-JUSTIFY: inter-ideograph; FONT-SIZE: 10.5pt; MARGIN: 0cm 0cm 0pt; FONT-FAMILY: "Times New Roman"; TEXT-ALIGN: justify}DIV.MyFav_1310453216462 LI.MsoNormal{TEXT-JUSTIFY: inter-ideograph; FONT-SIZE: 10.5pt; MARGIN: 0cm 0cm 0pt; FONT-FAMILY: "Times New Roman"; TEXT-ALIGN: justify}DIV.MyFav_1310453216462 DIV.MsoNormal{TEXT-JUSTIFY: inter-ideograph; FONT-SIZE: 10.5pt; MARGIN: 0cm 0cm 0pt; FONT-FAMILY: "Times New Roman"; TEXT-ALIGN: justify}DIV.MyFav_1310453216462 DIV.Section1{page: Section1}DIV.MyFav_1310453216462 OL{MARGIN-BOTTOM: 0cm}DIV.MyFav_1310453216462 UL{MARGIN-BOTTOM: 0cm}前不久竞赛卷上有这样一道填空题:
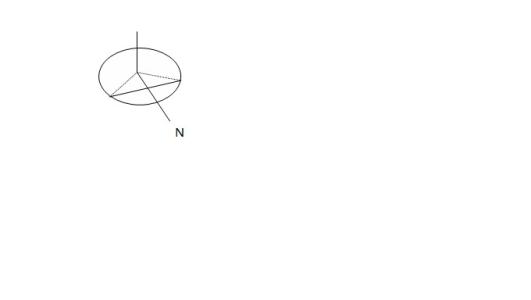
一列数按如图所示的规律排列,若第4行从左到右第2个数记为(4,9),那么数17应记作_________.
考完后,我是用数数的办法,得出答案的,虽做对了,但心里总觉得不是个滋味:本题如果是求一个较大的数(如168等)的位置,如果用死数的办法那又要数到猴年马月呀?于是,我作了如下的思考:
观察发现图中的数据排列有如下规律:
1. 从整体看,是从1开始的连续自然数排列;
2. 行数序号=该行数的个数;
3. 奇数行:从左到右依次增大;
4. 偶数行:从左到右依次减小;
5. 每行末端(最后一个数)具有如下特征:
奇行:右端数=;
偶行:左端数=.(n为行数序号)
解:首先确定数17所在的行:令=17,即=34。因为和是连续自然数,而乘积最接近34的连续自然数是5和6,但由于5×6<34,所以17应在第6行.在来确定数17是该行的第几个数:因为第5行末端是=15,而第6行的数有6个且从左到右是依次减小(即从右到左依次增大),所以17是第6行从左到右的第5个数,故17应记为(6,5).
有了这种解法,就不怕较大的数了,比如数2009在第几行,从左到右是第几个数,记作什么?令=2009,即=4018. 因为和是连续自然数,而乘积最接近4018的连续自然数是63和64,但由于63×64=4032>4018,所以2009应在第63行。现在来确定数2009是该行的第几个数:因为第62行末端数是=1953,而第63行的数有63个且从左到右是依次增大(即从右到左依次减小),所以2009是第63行从左到右的第56个数,故2009应记为(63,56).
事实上,对于任一正整数M,欲知它在第几行从左到右第几个数,1.用公式=M(M为正整数)找到最接近2M值的两个连续自然数a和b(a<b),若a×b <2M,则数M一定在第b行,若a×b >2M,则数M一定在第a行.2.确定该数是从左到右的第几个位置:先用公式=M,计算出b(或a)的前一行的最末端的数 ==P(或= =P)(P为正整数),再依规律2、3、4,考虑b(或a)的奇偶性,若b(或a)是奇数,则数M一定在从左到右的第M-P个位置;若b(或a)是偶数,则数M一定在从左到右的第b-(M-P)+1(或a-(M-P)+1)个位置.
注:此文发表于<数理天地>初中版2009年第7期.
爱华网本文地址 » http://www.aihuau.com/a/322651/73152078902.html

 爱华网
爱华网