(一)数的认识
整数【正数、、负数】
、一个物体也没有,用表示。和、、……都是自然数。自然数是整数。
、最小的一位数是,最小的自然数是。
、零上摄氏度记作℃;零下摄氏度记作℃。“”读作正四。“”读作负四。也可以写成。
、像、、这样的数都是正数。像、、、这样的数都是负数。
、既不是正数,也不是负数。正数都大于,负数都小于。
、通常情况下,比海平面高用正数表示,比海平面低用负数表示。
、通常情况下,盈利用正数表示,亏损用负数表示。
、通常情况下,上车人数用正数表示,下车人数用负数表示。
、通常情况下,收入用正数表示,支出用负数表示。
、通常情况下,上升用正数表示,下降用负数表示。
小数【有限小数、无限小数】
、分母是、、……的分数都可以用小数表示。一位小数表示十分之几,两位小数表示百分之几,三位小数表示千分之几……
、整数和小数都是按照十进制计数法写出的数,个、十、百……以及十分之一、百分之一……都是计数单位。每相邻两个计数单位间的进率都是。
、每个计数单位所占的位置,叫做数位。数位是按照一定的顺序排列的。
、小数的性质:小数的末尾添上“”或去掉“”,小数的大小不变。
、根据小数的性质,通常可以去掉小数末尾的“”,把小数化简。
、比较小数大小的一般方法:先比较整数部分的数,再依次比较小数部分十分位上的数,百分位上的数,千分位上的数,从左往右,如果哪个数位上的数大,这个小数就大。
、把一个数改写成用“万”或“亿”作单位的数,只要在万位或亿位右边点上小数点,再在数的后面添写“万”字或“亿”字。
、求小数近似数的一般方法:
()先要弄清保留几位小数;
()根据需要确定看哪一位上的数;
()用“四舍五入”的方法求得结果。
9、整数和小数的数位顺序表:
整 数 部 分
小数点
小 数 部 分
…
亿 级
万 级
个 级
数位
…
千亿位
百亿位
十亿位
亿
位
千万位
百万位
十万位
万
位
千
位
百
位
十
位
个
位
·
十分位
百分位
千分位
万分位
…
计数单位
…
千亿
百亿
十亿
亿
千万
百万
十万
万
千
百
十
个(一)
十分之一
百分之一
千分之一
万分之一
…
分数:
1、把单位“1”平均分成若干份,表示这样的一份或几份的数叫做分数。表示其中一份的数,是这个分数的分数单位。
2、两个数相除,它们的商可以用分数表示。即:a÷b=分之a(b≠0)
3、从小数和分数的意义可以看出,小数实际上就是分母是10、100、1000……的分数。
4、分数可以分为真分数和假分数。
5、分子小于分母的分数叫做真分数。真分数小于1。
6、分子大于或等于分母的分数叫做假分数。假分数大于或等于1。
7、分子和分母只有公因数1的分数叫做最简分数。
8、分数的基本性质:分数的分子和分母同时乘或除以相同的数(零除外),分数的大小不变。
9、小数的性质和分数的基本性质是一致的,应用分数的基本性质,可以通分和约分。
百分数:
1、表示一个数是另一个数的百分之几的数叫做百分数。百分数也叫百分率或百分比,百分数通常用“%”表示。
2、分数与百分数比较:3.分数、小数、百分数的互化。
不同点 相同点
分数 可以表示具体数量,可以有单位名称 表示两个数之间的关系
百分数 不可以表示具体数量,不可以有单位名称
()把分数化成小数,用分数的分子除以分母。
()把小数化成分数,先改写成分母是、、的分数,再约分。
()把小数化成百分数,先把小数点向右移动两位,然后添上百分号。
()把百分数化成小数,先去掉百分号,然后把小数点向左移动两位。
()把分数化成百分数,先把分数化成小数(除不尽时通常保留三位小数),再把小数化成百分数。
()把百分数化成分数,先把百分数改写成分数,能约分的要约成最简分数。
4、熟记常用三数的互化。
=0.5=50%
≈0.333=33.3%
≈0.667=66.7%
=0.25=25%
=0.75=75%
=0.2=20%
=0.4=40%
=0.6=60% =0.8=80%
≈0.167=16.7%
≈0.833=83.3%
=0.125=12.5%
=0.375=37.5%
=0.625=62.5%
=0.875=87.5%
=0.1=10% =0.3=30%
=0.7=70%
=0.9=90%
=0.05=5%
=0.15=15%
=0.35=35%
=0.45=45%
=0.55=55% =0.65=65%
=0.85=85%
=0.95=95%
=0.04=4%
=0.025=2.5%
=0.02=2%
=0.01=1%
5、出勤率表示出勤人数占总人数的百分之几。
合格率表示合格件数占总件数的百分之几。
成活率表示成活棵数占总棵数的百分之几。
6、求一个数比另一个数多百分之几,就是求一个数比另一个数多的占另一个数的百分之几。
7、多的÷“<?xml:namespace prefix = st1 />1”=多百分之几 少的÷“1”=少百分之几
8、应得利息是税前利息,实得利息是税后利息。
9、利息=本金×利率×时间
10、应得利息-利息税=实得利息
11、几折表示十分之几,表示百分之几十;几几折表示十分之几点几,表示百分之几十几。
12、原价×折扣=现价 现价÷原价=折扣 现价÷折扣=原价
13、几成表示十分之几表示百分之几十;几成几表示十分之几点几,表示百分之几十几。
因数与倍数【素数、合数、奇数、偶数】
1、4×3=12,12是4的倍数,12也是3的倍数,4和3都是12的因数。
2、一个数最小的倍数是它本身,没有最大的倍数。一个数倍数的个数是无限的。
3、一个数最小的因数是1,最大的因数是它本身。一个数因数的个数是有限的。
4、5的倍数:个位上的数是5或0。
2的倍数:个位上的数是2、4、6、8或0。2的倍数都是双数。
3的倍数:各位上数的和一定是3的倍数。
5、是2的倍数的数叫做偶数。不是2的倍数的数叫做奇数。
6、一个数,如果只有1和它本身两个因数,这样的数就叫做素数(或质数)。
7、一个数,如果除了1和它本身还有别的因数,这样的数就叫做合数。
8、在1—20这些数中: (1既不是素数,也不是合数)
奇数:1、3、5、7、9、11、13、15、17、19。
偶数:2、4、6、8、10、12、14、16、18、20。
素数:2、3、5、7、11、13、17、19。(共8个,和为77。)
合数:4、6、8、9、10、12、14、15、16、18、20。(共11个,和为132。)
9、最小的奇数是1,最小的偶数是0,最小的素数是2,最小的合数是4。
10、如果两个数是倍数关系,则大数是最小公倍数,小数是最大公因数。
11、如果两个数只有公因数1,则最大公因数是1,最小公倍数是它们的乘积。
因数与倍数【素数、合数、奇数、偶数】
1、4×3=12,12是4的倍数,12也是3的倍数,4和3都是12的因数。
2、一个数最小的倍数是它本身,没有最大的倍数。一个数倍数的个数是无限的。
3、一个数最小的因数是1,最大的因数是它本身。一个数因数的个数是有限的。
4、5的倍数:个位上的数是5或0。
2的倍数:个位上的数是2、4、6、8或0。2的倍数都是双数。
3的倍数:各位上数的和一定是3的倍数。
5、是2的倍数的数叫做偶数。不是2的倍数的数叫做奇数。
6、一个数,如果只有1和它本身两个因数,这样的数就叫做素数(或质数)。
7、一个数,如果除了1和它本身还有别的因数,这样的数就叫做合数。
8、在1—20这些数中: (1既不是素数,也不是合数)
奇数:1、3、5、7、9、11、13、15、17、19。
偶数:2、4、6、8、10、12、14、16、18、20。
素数:2、3、5、7、11、13、17、19。(共8个,和为77。)
合数:4、6、8、9、10、12、14、15、16、18、20。(共11个,和为132。)
9、最小的奇数是1,最小的偶数是0,最小的素数是2,最小的合数是4。
10、如果两个数是倍数关系,则大数是最小公倍数,小数是最大公因数。
11、如果两个数只有公因数1,则最大公因数是1,最小公倍数是它们的乘积。
(二)数的运算
计算法则【整数、小数、分数】
1、计算整数加、减法要把相同数位对齐,从低位算起。
2、计算小数加、减法要把小数点对齐,从低位算起。
3、小数乘法:
(1)先按整数乘法算出积是多少,看因数中一共有几位小数,就从积的右边起数出几位,点上小数点。
(2)注意:在积里点小数点时,位数不够的,要在前面用0补足。
4、小数除法:
(1)商的小数点要和被除数的小数点对齐;
(2)有余数时,要在后面添0,继续往下除;
(3)个位不够商1时,要在商的整数部分写0,点上小数点,再继续除。
(4)把除数转化成整数时,除数的小数点向右移动几位,被除数的小数点也要向右移动几位。
(5)当被除数的小数位数少于除数的小数位数时,要在被除数的末尾用0补足。
5、一个小数乘10、100、1000……只要把这个小数的小数点向右移动一位、两位、三位……
6、一个小数除以10、100、1000……只要把这个小数的小数点向左移动一位、两位、三位……
7、分数加、减法:
(1)同分母分数相加减,把分子相加减,分母不变。
(2)异分母分数相加减,要先通分化成同分母分数,然后再相加减。
8、分数大小的比较:
(1)同分母分数相比较,分子大的大,分子小的小。
(2)异分母的分数相比较,先通分然后再比较;若分子相同,分母大的反而小。
9、分数乘分数,用分子相乘的积作分子,分母相乘的积作分母。
10、甲数除以乙数(0除外),等于甲数乘乙数的倒数。
四则运算关系
加法
一个加数=和-另一个加数
减法
被减数=差+减数 减数=被减数-差
乘法
一个因数=积÷另一个因数
除法
被除数=商×除数 除数=被除数÷商
两个规律
1、除法的商不变规律:被除数和除数同时乘或除以相同的数(0除外),商不变。
2、乘法的积不变规律:如果一个因数乘几,另一个因数则除以几,那么它们的积不变。
两个规律
、除法的商不变规律:被除数和除数同时乘或除以相同的数(除外),商不变。
、乘法的积不变规律:如果一个因数乘几,另一个因数则除以几,那么它们的积不变。
简便计算
、运算定律:
运算定律
用字母表示
加法交换律
++
加法结合律
(+)+++
乘法交换律
××
乘法结合律
(×)×××
乘法分配律
(+)××+×
减法运算规律
---(+)
除法运算规律
÷÷÷(×)
、乘、除法的互化。(小技巧:符号是相反的;两个数相乘得数与的关系。)
()÷×
()×÷
()÷×;
()×÷
()÷×
()×÷
()÷×
()×÷
()÷×
()×÷
()÷×
()×÷
、求近似数的方法。
()四舍五入法。()进一法。()去尾法。
用字母表示数
、在一个含有字母的式子里,数字和字母、字母和字母相乘时,中间的乘号可以记作“·”,也可以省略不写。在省略数字与字母之间的乘号时,要把数字写在字母的前面。
、与意义不同:表示两个相加,表示两个相乘。即:+,×。
、用字母表示数:
()用字母表示任意数:如
()用字母表示常见的数量关系:如
()用字母表示运算定律:如++
()用字母表示计算公式:
方程与等式
1、含有未知数的等式叫做方程。
2、使方程左右两边相等的未知数的值,叫做方程的解。
3、求方程的解的过程,叫做解方程。
4、方程和等式的联系与区别:
方 程
等 式
联 系
方程一定是等式,等式不一定是方程
区 别
含有未知数
不一定含有未知数
5、等式的基本性质(一)
等式两边同时加上(或减去)一个相同的数,所得结果仍然是等式。
6、等式的基本性质(二)
等式两边同时乘(或除以)一个不等于零的数,所得结果仍然是等式。
7、列方程解应用题的一般步骤:
(1)弄清题意,找出未知数并用X表示。
(2)找出应用题中数量间的相等关系,并列出方程。
(3)求出方程的解。
(4)检验或验算,写出答案。
(四)正比例与反比例
比和比例
1、比和比例的联系与区别:
比
与
比
例

的
区
别
1、意义不同
比的意义
两个数相除又叫做两个数的比。
比例的意义
表示两个比相等的式子叫做比例。
2、名称不同
比的名称
两点读作比,比号前面的数叫做比的前项,比号后面的数叫做比的后项。
比例的名称
组成比例的四个数叫做比例的项,两端的两项叫做比例的的外项,中间的两项叫做比例的内项。
3、性质不同
比的性质
比 的前项和后项同时乘或者除以相同的数(0除外),比值不变。
比例的性质
在比例里,两个外项的积等于两个内项的积。
4、应用不同
应用比的意义
求比值。
应用比的性质
化简比。
应用比例的意义
判断两个不能否组成比例。
应用比例的性质
不但可以判断两个比能否组成比例,还可以解比例。
2、比同分数、除法的联系与区别:
比
分数
除法
联
系
前项
分子
被除数
比号
分数线
除号
后项
分母
除数
比值
分数值
商
比的基本性质
分数的基本性质
除法的商不变性质
区
别
比表示两个数之间的关系。
分数表示一个数。
除法表示一种运算。
3、求比值与化简比的区别:
一 般 方 法
结 果
求比值
根据比值的意义,用前项除以后项。
是一个数。可以是整数、小数或分数。
化简比
根据比的基本性质,把比的前项和后项都乘或除以相同的数(零除外)。
是一个比。它的前项和后项都是整数,并且是互质数。
4、化简比:
(1)整数比的化简方法是:用比的前项和后项同时除以它们的最大公约数。
(2)小数比的化简方法是:先把小数比化成整数比,再按整数比化简方法化简。
(3)分数比的化简方法是:用比的前项和后项同时乘以分母的最小公倍数。
5、比例尺:我们把图上距离和实际距离的比叫做这幅图的比例尺。
6、比例尺=图上距离︰实际距离
正比例、反比例
1、正比例:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系就叫做正比例关系。
2、反比例:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系就叫做反比例关系。
3、正比例与反比例的区别:
正 比 例
反 比 例
相 同 点
都有两种相关联的量,一种量变化,另一种量也随着变化。
不 同 点
商一定
积一定
x×y=k(一定)
、比同分数、除法的联系与区别:
比
分数
除法
联
系
前项
分子
被除数
比号
分数线
除号
后项
分母
除数
比值
分数值
商
比的基本性质
分数的基本性质
除法的商不变性质
区
别
比表示两个数之间的关系。
分数表示一个数。
除法表示一种运算。
3、求比值与化简比的区别:
一 般 方 法
结 果
求比值
根据比值的意义,用前项除以后项。
是一个数。可以是整数、小数或分数。
化简比
根据比的基本性质,把比的前项和后项都乘或除以相同的数(零除外)。
是一个比。它的前项和后项都是整数,并且是互质数。
4、化简比:
(1)整数比的化简方法是:用比的前项和后项同时除以它们的最大公约数。
(2)小数比的化简方法是:先把小数比化成整数比,再按整数比化简方法化简。
(3)分数比的化简方法是:用比的前项和后项同时乘以分母的最小公倍数。
5、比例尺:我们把图上距离和实际距离的比叫做这幅图的比例尺。
6、比例尺=图上距离︰实际距离
正比例、反比例
1、正比例:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系就叫做正比例关系。
2、反比例:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系就叫做反比例关系。
3、正比例与反比例的区别:
正 比 例
反 比 例
相 同 点
都有两种相关联的量,一种量变化,另一种量也随着变化。
不 同 点
商一定
积一定
x×y=k(一定)
第二单元空间与图形
(一)图形的认识、测量
量的计量
、长度单位是用来测量物体的长度的。常用的长度单位有:千米、米、分米、厘米、毫米。
、长度单位:()
千米米
米分米
分米厘米
厘米毫米
米厘米
、面积单位是用来测量物体的表面或平面图形的大小的。常用的面积单位有:平方千米、公顷、平方米、平方分米、平方厘米。
、测量和计算土地面积,通常用公顷作单位。边长米的正方形土地,面积是公顷。
、测量和计算大面积的土地,通常用平方千米作单位。边长米的正方形土地,面积是平方千米。
、面积单位:()
平方千米公顷
公顷平方米
平方米平方分米
平方分米平方厘米
、体积单位是用来测量物体所占空间的大小的。常用的体积单位有:立方米、立方分米(升)、立方厘米(毫升)。
、体积单位:()
立方米立方分米
立方分米立方厘米
升毫升
、常用的质量单位有:吨、千克、克。
、质量单位:
吨千克
千克克
、常用的时间单位有:世纪、年、季度、月、旬、日、时、分、秒。
、时间单位:()
世纪年
年个月
年个季度
个季度个月
个月旬
大月天
小月天
平年二月天
闰年二月天
天小时
小时分
分秒
、高级单位的名数改写成低级单位的名数应该乘以进率;
低级单位的名数改写成高级单位的名数应该除以进率。
14、常用计量单位用字母表示:
千米:km
米:m
分米:dm
厘米:cm
毫米:mm
吨:t
千克:kg
克:g
升:l
毫升:ml
平面图形【认识、周长、面积】
1、用直尺把两点连接起来,就得到一条线段;把线段的一端无限延长,可以得到一条射线;把线段的两端无限延长,可以得到一条直线。线段、射线都是直线上的一部分。线段有两个端点,长度是有限的;射线只有一个端点,直线没有端点,射线和直线都是无限长的。
2、从一点引出两条射线,就组成了一个角。角的大小与两边叉开的大小有关,与边的长短无关。角的大小的计量单位是(°)。
3、角的分类:小于90度的角是锐角;等于90度的角是直角;大于90度小于180度的角是钝角;等于180度的角是平角;等于360度的角是周角。
4、相交成直角的两条直线互相垂直;在同一平面不相交的两条直线互相平行。
5、三角形是由三条线段围成的图形。围成三角形的每条线段叫做三角形的边,每两条线段的交点叫做三角形的顶点。
6、三角形按角分,可以分为锐角三角形、直角三角形和钝角三角形。按边分,可以分为等边三角形、等腰三角形和任意三角形。
7、三角形的内角和等于180度。
8、在一个三角形中,任意两边之和大于第三边。
9、在一个三角形中,最多只有一个直角或最多只有一个钝角。
10、四边形是由四条边围成的图形。常见的特殊四边形有:平行四边形、长方形、正方形、梯形。
11、圆是一种曲线图形。圆上的任意一点到圆心的距离都相等,这个距离就是圆的半径的长。通过圆心并且两端都在圆的线段叫做圆的直径。
12、有一些图形,把它沿着一条直线对折,直线两侧的图形能够完全重合,这样的图形就是轴对称图形。这条直线叫做对称轴。
13、围成一个图形的所有边长的总和就是这个图形的周长。
14、物体的表面或围成的平面图形的大小,叫做它们的面积。
15、平面图形的面积计算公式推导:
【1】平行四边形面积公式的推导过程?
(1)把平行四边形通过剪切、平移可以转化成一个长方形。
(2)长方形的长等于平行四边形的底,长方形的宽等于平行四边形的高,长方形的面积等于平行四边形的面积。
(3)因为:长方形面积=长×宽,所以:平行四边形面积=底×高。即:S=ah。
【2】三角形面积公式的推导过程?
(1)用两个完全一样的三角形可以拼成一个平行四边形。
(2)平行四边形的底等于三角形的底,平行四边形的高等于三角形的高,三角形面积等于和它等底等高的平行四边形面积的一半
(3)因为:平行四边形面积=底×高,所以:三角形面积=底×高÷2。即:S=ah÷2。
【3】画图说明圆面积公式的推导过程
(1)把圆分成若干等份,剪开后,拼成了一个近似的长方形。
(2)长方形的长相当于圆周长的一半,宽相当于圆的半径。
(3)因为:长方形面积=长×宽,所以:圆面积=πr×r=πr2。即:S=πr2。
16、平面图形的周长和面积计算公式:
长方形周长=(长+宽)×2
长方形面积=长×宽
正方形周长=边长×4
正方形面积=边长×边长
平行四边形面积=底×高
三角形面积=底×高÷2
梯形面积=(上底+下底)×高÷2
C=πd
C=2πr
r=d÷2
r=C÷2π
d=2r
d=÷π
S=πr2
17、常用数据:
常用π值
常用平方数
2π=6.28
3π=9.42
4π=12.56
5π=15.70
6π=18.84
7π=21.98
8π=25.12
9π=28.26
10π=31.4
12π=37.68
15π=47.1
16π=50.24
18π=56.52
20π=62.8
25π= 78.5
32π=100.48
2.25π=7.065
6.25π=19.625
112=121
122=144
152=225
252=625
立体图形【认识、表面积、体积】
1、长方体、正方体都有6个面,12条棱,8个顶点。正方体是特殊的长方体。
2、圆柱的特征:一个侧面、两个底面、无数条高。
3、圆锥的特征:一个侧面、一个底面、一个顶点、一条高。
4、表面积:立体图形所有面的面积的和,叫做这个立体图形的表面积。
5、体积:物体所占空间的大小叫做物体的体积。容器所能容纳其它物体的体积叫做容器的容积。
6、圆柱和圆锥三种关系:
(1)等底等高:体积1:3
(2)等底等体积:高1:3
(3)等高等体积:底面积1:3
7、等底等高的圆柱和圆锥:
(1)圆锥体积是圆柱的三分之一,
(2)圆柱体积是圆锥的3倍,
(3)圆锥体积比圆柱少三分之二,
(4)圆柱体积比圆锥多2倍。
8、立体图形公式推导:
【1】圆柱的侧面展开后得到一个什么图形?这个图形的各部分与圆柱有何关系?(圆柱侧面积公式的推导过程)
(1)圆柱的侧面展开后一般得到一个长方形。
(2)长方形的长相当于圆柱的底面周长,长方形的宽相当于圆柱的高。
(3)因为:长方形面积=长×宽,所以:圆柱侧面积=底面周长×高。
(4)圆柱的侧面展开后还可能得到一个正方形。
正方形的边长=圆柱的底面周长=圆柱的高。
【2】我们在学习圆柱体积的计算公式时,是把圆柱转化成以前学过的一种立体图形(近似的)进行推导的,请你说出这种立体图形的名称以及它与圆柱体有关部分之间的关系?
(1)把圆柱分成若干等份,切开后拼成了一个近似的长方体。
(2)长方体的底面积等于圆柱的底面积,长方体的高等于圆柱的高。
(3)因为:长方体体积=底面积×高,所以:圆柱体积=底面积×高。
即:V=Sh。
【3】请画图说明圆锥体积公式的推导过程?
(1)找来等底等高的空圆锥和空圆柱各一只。
(2)将圆锥装满沙子,倒入圆柱中,发现三次正好装满,将圆柱里的沙子倒入圆锥中,发现三次正好倒完。
(3)通过实验发现:圆锥的体积等于和它等底等高的圆柱体积的三分之一;圆柱的体积等于和它等底等高的圆锥体积的三倍。即:V= Sh。
9、立体图形的棱长总和、表面积、体积计算公式:
长方体棱长总和=(长+宽+高)×4
长方体表面积=(长×宽+长×高+宽×高)×2
长方体体积=长×宽×高
正方体棱长总和=棱长×12
正方体表面积=棱长×棱长×6
正方体体积=棱长×棱长×棱长
圆柱侧面积=底面周长×高
圆柱表面积=侧面积+底面积×2
圆柱体积=底面积×高
圆锥体积:V=Sh/3
(二)图形与变换
1、变换图形位置的方法有平移、旋转等,在变换位置时,每个图形的相应顶点、线段、曲线应同步平移,旋转相同的角度。
2、不改变图形的形状,只改变它的大小时,通常要使每个图形的要素,如长方形的长与宽,三角形的底与高等同时按相同比例放大或缩小。
3、对称图形是对称轴两边的图形经对折后能够完全重合,而不是完全相同。
(三)图形与位置
1、当我们处在实际生活及情景中,面对教短距离时,通常用上、下、前、后来描述具体位置。
2、当我们面对地图、方位图时,通常用东、西、南、北,南偏东、北偏东……来描述方向。再结合所示比例尺计算出具体距离,把方向与距离结合起来确定位置。
第三单元 统计与可能性
(一)统计
1、我们通常都是通过打勾、画圆、划“正”字的方法进行数据的收集和整理。
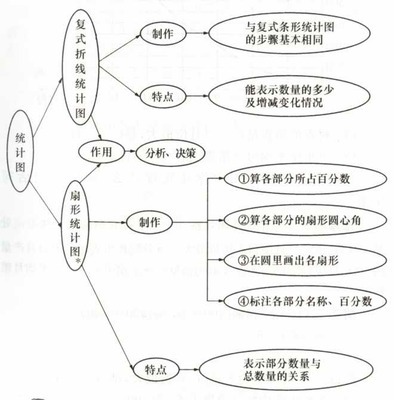
2、常见的统计图有条形统计图、折线统计图和扇形统计图三种。
3、条形统计图的特点:从图中能清楚地看出各种数量的多少,便于比较。
4、折线统计图的特点:不但能看出各种数量的多少,而且还能够清楚地表示出数量增减变化的情况。
5、扇形统计图的特点:表示各部分和总数之间,以及部分与部分之间的关系。
6、中位数、众数、平均数
名称
意义
计算方法
中位数
一组数中间的一个数或中间两个数的平均数。
中间的一个数或中间两个数的和÷2
众数
一组数中出现次数最多的数。
出现次数最多的数
平均数
反映一组数的总体水平的数据。
平均数=总数÷份数
(二)可能性
1、
事件状态
生活情景
数学情景
一定会发生
太阳从东方升起
从5个红球中摸出一个红球
一定不会发生
鸭子会讲话
从5个红球中摸出一个白球
可能发生
今天会下雨
从5个红球,1个白球中摸出一个白球
2、在可能性相同的情况下,比赛游戏规则是公平的。
 爱华网
爱华网