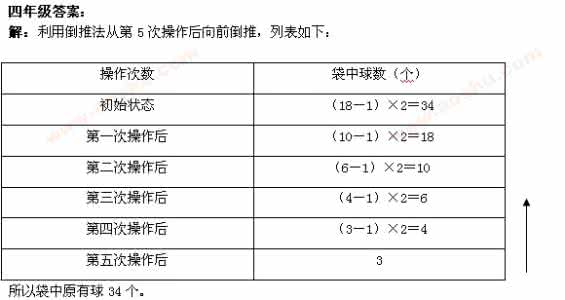
3、小悦掷出了2枚骰子,掷出的2个数字之和恰好等于10的概率有多少?【答案】事件A:2个数字之和是10,有三种情况,即:(4+6)、(5+5)、(6+4);而每种情况的概率都是; 4、6名小朋友在操场上做游戏.他们被老师分成3组,每组2个人.请问:赵倩和孙莉恰好分到了同一组的概率是多少?【答案】方法1:排列组合思想
事件A:赵倩和孙莉恰好分到了同一组,那么A有三种情况,可能在第一组、第二组、第三组三种可能性;所以一共的可能性共有种;
全事件S:将6人分成3组,S有种可能;
方法2:枚举法
假设给这6名小朋友编号为1、2、3、4、5、6,赵倩和孙莉编号分别为1和2;
事件A:赵倩和孙莉恰好分到了同一组(无排列顺序列举),[(1、2)、(3、4)、(5、6)];[(1、2)、(3、5)、(4、6)];[(1、2)、(3、6)、(4、5)],三种情况;
全事件S:将6人分成3组(无排列顺序列举),即:
(1)1和2同组:[(1、2)、(3、4)、(5、6)];[(1、2)、(3、5)、(4、6)];[(1、2)、(3、6)、(4、5)];3种情况;
(2)1和3同组:[(1、3)、(2、4)、(5、6)];[(1、3)、(2、5)、(4、6)];[(1、3)、(2、6)、(4、5)];3种情况;
(3)1和4同组:同理列举有3种;
(4)1和5同组:同理列举有3种;
(5)1和6同组:同理列举有3种;
所以全事件S一共有3×5=15种
其实也可以这样来理解,针对于1号小朋友来说,他可能和2、3、4、5、6号同组,总共有5种情况,在每组情况概率都相同的情况下,1号和2号同组的概率为5、一块牧场长满了草,每天均匀生长。这块牧场的草可供10头牛吃40天,供15头牛吃20天。可供25头牛吃多少天?【答案】假设1头牛1天吃草的量为1份
(1)每天新生的草量为:(10×40-15×20)÷(40-20)=5(份);
(2)原来的草量为:10×40-40×5=200(份);
(3)安排5头牛专门吃每天新长出来的草,这块牧场可供25头牛吃:200÷(25-5)=10(天)。6、某游乐场在开门前已经有100个人排队等待,开门后每分钟来的游人数是相同的,一个入口处每分钟可以放入10名游客,如果开放2个入口20分钟后就没有人排队,现在开放8个入口处,每分钟关闭一个门,那么开门后几分钟就没人排队了?【答案】(1)每分钟来的游人数是:(20×10×2-100)÷20=15(名)游客
(2)第1分钟期间开了8个门,所以放入80名游客,还剩:100+15-80=35(名)游客
(3)第2分钟期间开7个门:由于70大于35+15=50,所以肯定是在第2分钟期间的某个时间就没人排队了,不妨设从第2分钟开始t分钟后就没人排队了,故t分钟内新来了15t个游客,7个门放入了7×10t个游客,所以由方程15t+35=7×10t,解得t=,即在 分钟后就没人排队了。7、一个两位数等于它的数字和的6倍,求这个两位数.【答案】两位数字和介于1-18之间,记这个两位数为 ,则: 即这个两位数为548、今年是2008年,小王说:“我的年龄正好与我出生那年年份的四个数字之和相同”.请问:小王今年多大?
9、
10、 11、已知 ,求所有满足条件的六位数12、求能被26整除的六位数13、师徒三人合做承包一项工程,8天能够全部完成。已知师傅单独做所需的天数与两个徒弟合做所需天数相同。师傅与徒弟甲合做所需的天数的4倍与徒弟乙单独完成这项工程所需的天数相同。问:两徒弟单独完成工程各需多少天?14、要用甲、乙两根水管灌满一个水池,开始只打开甲管,9 min后打开乙管,再过了4 min已灌入水池的水,再经过10 min,灌入的水已占水池的。这时关掉甲管只开乙管,从开始到灌满水池,乙共用了多少分钟?15、 16、 17、有一牧场,已知养牛27头,6天把草吃尽;养牛23头,9天把草吃尽。如果养牛21头,那么几天能把牧场上的草吃尽呢?【答案】先假设1头牛1天所吃的牧草为1,那么就有:
(1)27头牛6天所吃的牧草为:27×6=162 (这162包括牧场原有的草和6天新长的草。)
(2)23头牛9天所吃的牧草为:23×9=207 (这207包括牧场原有的草和9天新长的草。)
(3)1天新长的草为:(207-162)÷(9-6)=15
(4)牧场上原有的草为:27×6-15×6=72
(5)每天新长的草足够15头牛吃,21头牛减去15头,剩下6头吃原牧场的草:72÷(21-15)=72÷6=12(天)
所以养21头牛,12天才能把牧场上的草吃尽18、有三块草地,面积分别是4公顷、8公顷和10公顷.草地上的草一样厚而且长得一样快.第一块草地可供24头牛吃6周,第二块草地可供36头牛吃12周.问:第三块草地可供50头牛吃几周?【答案】先假设1头牛1天所吃的牧草为1,那么就有:
(1)24头牛6周所吃的牧草为:24×6=144(4公顷+4公顷6周长的草),即2公顷+2公顷6周长的草量为:144÷2=72;
(2)36头牛12周所吃的牧草为:36×12=432(8公顷+8公顷12周长的草),即2公顷+2公顷12周长的草量为:432÷4=108;
(3)2公顷16周长的草量为:108-72=36,即2公顷1周长的草为:36÷6=6;所以对于每2公顷新长的草量刚好配6头牛吃完。
(4)对于面积为4公顷可供24头牛吃6周,其中刚好配有6×2=12头牛吃新长的草量,那么还剩下24-12=12头牛吃4公顷原有的草量用了6周,即原4公顷的草量为:12×6=72,所以得出10公顷原有的草量为:72× =180;
(5)对于10公顷的场地,其中新长的草量可供10÷2×6=30头牛来吃,而剩下的50-30=20头牛负责吃10公顷原有的草量,即一共能吃的周数:180÷20=9周。所以第三块草地可供50头牛吃9周。19、如下图,在三角形ABC中,BD=2AD,AG=2CG,BE=EF=FC=BC,求四边形DGFE面积占三角形ABC的几分之几? 【答案】20、如图正方形ABCD的边长为10厘米,E为AD中点,F为CE中点,G为BF中点,求三角形BDG的面积。【答案】 21、一个五位数a,分别被2,3,4,5,6,7,8,9,10除时,余数都等于1,则a的最大值等于( )。【答案】首先找到2,3,4,5,6,7,8,9,10的最小公倍数,那么要想这个五位数分别被这些数除都余1,那么这个数就一定要等于最小公倍数的倍数加1,所以根据这个性质进行解题分析和切入。
2,3,4,5,6,7,8,9,10的最小公倍数等于:
7×8×9×10÷(8,10)=2520
于是有表达式:
a=2520k+1,k=1,2,2……
当a为五位数时,a的最大值为 =2520×39+1=9828122、自然数m除13511,13903和14589的余数都相同.则m的最大值是( ) 【答案】一个数除其他不同的数所得的余数相等,那么这个数一定能整除这些其他不同数的差,根据这个性质,解决这道题便迎刃而解了。
由于m除13511,13903和14589的余数都相同,所以m整除13903-13511= 392;m整除14589-14903= 686;m整除14589 -13511=1078。
所以,m一定是392、686、1078的公约教.要求m的最大值,就是求392,686,1078的最大公约数.
因为392=7 2×2 3,686=7 3×2,1078=7 2×2×13
所以(392,686,1078)= 7 2×2=98
即m的最大值为98.23、计算:24、25、某些数除以 11余 1,除以 13余 3,除以 15余 13,那么这些数中最小的数是_______.
【答案】设这个数为M,所以M=11x+1=13y+3=15z+13,其中x、y、z都是自然数;所以11x=11y+2y+2=11z+4z+11+1,即:
也就是y+1和4z+1都能够被11整除;其中满足条件的y最小为10
当y=10时,x=12,z=8也满足条件
所以满足题意的最小的数为13×10+3=13326、在自然数 1—2011中,最多可以取出________个数,使得这些数中任意四个数的和都不能被 11整除。【答案】分析这任意这个数不能被11整除的情况,其中余数为1和2的肯定全部都满足条件(因为2+2+2+2=8<11),那么2011÷11=182...9,所以得出1-2011中,余数是1和2的数有182×2+2=366个;
另外分析余数是3的情况,最多允许有2个,因为当有3个余数为3的情况时,有3+3+3+2=1能被11整除,不满足情况,所以余数为3的数最多只能有2个;最后考虑能够被11整除的数,最多只能有3个,因为超过4个话就有整除的情况发生;综上所述:最多可以取出满足条件的数有366+3+2=371个。27、某商场销售MP4,去年按定价的90℅出售,能获得20℅的利润,今年由于进价降低,按去年定价的80℅出售,能获得25℅的利润.今年进价是去年进价的______℅.28、某停车场中共有三轮摩托车,四轮小轿车和六轮大卡车30辆,各种轮子共116个.已知四轮小轿比六轮大卡车的5倍多2辆,那么这个停车场中共有______辆小轿车.29、如图3,已知正方形ABCD 和正方形CEFG 的边长分别是8 厘米和6 厘米,那么阴影部分的面积是___平方厘米. 30、如图4 所示的两个同心圆的半径分别为R 和r,R 和r 都是自然数,若圆环(阴影部分)的面积是493π,则R-r=___. 31、沪宁高铁通车后,一列动车早晨8时从南京开往上海,途中停靠5个车站,每站各停车2分钟.8时25分一列高速列车也从南京开往上海,途中不停车,高速列车的速度比动车快,结果两车同时到达上海.高速列车从南京开到上海用时___分钟.32、小明下午放学后在家看动画片,这时刚好是6点整,此刻钟面上的时针反向成一条直线,当他看完动画片后,时针和分针刚好又一次反向成一条直线,则此刻是___时___分.33、在 1,2,3,4,…100这100个数中取出两个数,使这两个数的和能被4整除,最多有___种不同的取法.【答案】将1、2、3....100这100个数字分成四类:
(1)能够被4整除的有25个;
(2)被4除余数为1的有25个;
(3)被4除余数为2的有25个;
(4)被4除余数为3的有25个;
取出两个数,能够被4整除,可以从(1)中取出2个数字,即种;
也可以从(2)和(4)中各取一个,即25×25=625种;也可以从(3)中取出两个,即种;所以一共有300+625+300=1225种取法。34、用红、黄、蓝三种颜色把图11中的8个小圆圈涂上颜色,每个圆圈只涂一种颜色,并且有连线的两个圆圈不能同色,那么不同的涂法有___种. 【答案】中间两个圆圈连线最多,可以从这里下手,不妨用字母表示图中的圆圈,如图在A圆圈中涂红色,那么B、C、D三个圆圈的涂色方法有6种;A圆圈可以涂上红黄蓝三种颜色中的任何一种,所以A、B、C、D四个圆圈的涂色方法有6×3=18种情况;又因为A、B、C、D又都有一条线分别与E、F、G、H相连,所以E、F、G、H又各有2中涂法;所以由此可知,不同的涂法共有18×2×2×2×2=288种。35、某天上海世博会中国馆入口处已有945名游客等候检票进馆.此时,每分钟还有若干人前来入口处准备进馆.这样,如果打开4个检票口,15分钟游客可以全部进馆;如果打开8个检票口,7分钟游客可以全部进馆.现在要求在5分钟内所有游客全部进馆,需要打开___个检票口.36、有三块草地,面积分别是5,15,25亩。草地上的草一样厚,而且长得一样快。第一块草地可供l0头牛吃30天,第=块草地可供28头牛吃45天,则第三块草地可供 头牛吃60天。37、在图10和乘法算式中,每个□表示一个数字,则计算所得的乘积是___.【答案】如下图所示: 38、将 1~9这九个数字分别填入下列算式中的□中,使等式成立:(每个数字只能用一次) □□□×□□=□□×□□=4002【答案】将4002分解为2×3×23×29,由此可知,将4002分解成两个两位数的乘积有2种,即4002=58×69=46×87;而将4002分解为一个两位数与一个三位数的乘积有2种,即4002=23×174=29×138;所以根据每个数字只能用一次,所以填法只有一种,即:23×174=58×69=400239、如果 a,b 均为质数,且 3a+7b=41,则 a+b=?40、已知五个数依次是16 , 24 ,15,25,20 它们每相邻的两个数相乘得四个数,这四个数每相邻的两个数相乘得三个数。这三个数每相邻的两个数相乘得两个数,这两个数相乘得一个数。请问最后这个数从个位起向左数,可以连续地数到几个0? 41、图中,长方形ABCD的长是6 cm,宽是4 cm,求阴影部分的面积。 【答案】这道题可以利用容斥原理来解答,因为扇形ABE和扇形ADF的重叠部分为阴影的上部分,所以它们的和相当于就是在长方形的基础上多出了阴影部分;
因此阴影部分的面积等于扇形ABE和扇形ADF的面积之和减去长方形ABCD的面积,即:

42、如图所示,长方形ABCD内的阴影部分的面积之和为70,AB=8,AD=15四边形EFGO的面积为______.
【答案】根据容斥关系:
四边形EFGO的面积=三角形AFC+三角形DBF-白色部分的面积
三角形AFC+三角形DBF=长方形面积的一半,即60,
白色部分的面积等于长方形面积减去阴影部分的面积,即120-70=50
所以四边形EFGO的面积=60-50=1043、今年兄弟二人年龄之和为55岁,哥哥某一年的岁数与弟弟今年的岁数相同,那一年哥哥的岁数恰好是弟弟岁数的2倍,请问哥哥今年多少岁?44、爸爸和女儿两人岁数加起来是91岁,当爸爸岁数是女儿现在岁数两倍的时候,女儿岁数是爸爸现在岁数的 ,那么爸爸现在的年龄是多少岁,女儿现在年龄是多少岁?
 爱华网
爱华网